tìm x
2x - 3.( x - 4) = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Biến đổi về dạng (x - 3)(x + 2) = 0. Tìm được x ∈ { - 2 ; 3 }
b) Thu gọn về dạng -2x + 3 = 0. Tìm được x = 3 2

\(2x\left(4x+3\right)+5=x\left(8x+4\right)+1\\ \Leftrightarrow8x^2+6x+5=8x^2+4x+1\\ \Leftrightarrow8x^2-8x^2+6x-4x=1-5\\ \Leftrightarrow2x=-4\\ \Leftrightarrow x=-4:2\\ \Leftrightarrow x=-2\)
Vậy \(x=-2\)

\(2x\left(2x-1\right)-\left(2x+5\right)^2=0\)
=>\(4x^2-2x-4x^2-20x-25=0\)
=>-22x-25=0
=>22x+25=0
=>22x=-25
=>\(x=-\dfrac{25}{22}\)

a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình  không thể có nghiệm x = - 1
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 

Điều kiện x ≠ 2 và x ≠ 0
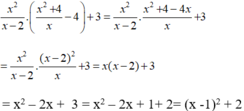
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.

a) x ≠ 0, x ≠ 2.
b) Ta có C = x 2 - 2x + 3.
c) Ta có C = x 2 - 2x + 3 = ( x - 1 ) 2 + 2 ≥ 2.
Từ đó suy ra giá trị nhỏ nhất của C = 2 khi x = 1.

Ta có:
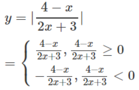
Trước hết, ta vẽ đồ thị (C) của hàm số
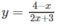
TXĐ: D = R \ {−3/2}.
Vì 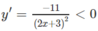
với mọi nên hàm số nghịch biến trên các khoảng
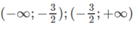
Bảng biến thiên:
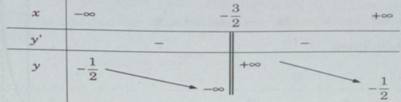
Tiệm cận đứng x = −3/2
Tiệm cận ngang y = −1/2
Đồ thị (C) đi qua các điểm (−2;−6),(−1;5),(0;4/3),(4;0)
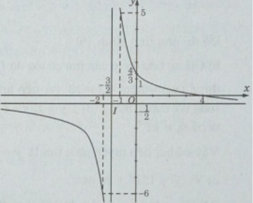
Để vẽ đồ thị (C’) của hàm số , ta giữ nguyên phần đồ thị (C) nằm phía trên trục hoành và lấy đối xứng phần đồ thị (C) nằm phía dưới trục hoành qua trục hoành.
2x-3.(x-4)=0
2x-3x-3.4=0
x(2-3)-12=0
x.(-1)=0+12
-x=12
x=-12
vậy...
\(2x-3\left(x-4\right)=0\)
\(\Leftrightarrow2x-3x=-12\)
\(\Rightarrow x=12\)