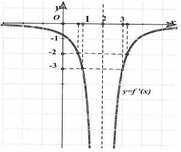
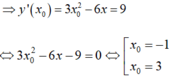Cho hàm số y= x^3 - 3x có tiếp tuyến song song với đường thẳng y= 9x + 10 thì số tiếp tuyến đó là ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(-9x+y-5=0\Leftrightarrow y=9x+5\)
\(\Rightarrow\) Đường thẳng d có hệ số góc bằng 9
\(y'=3x^2-6x\)
Tiếp tuyến song song d nên có hệ số góc thỏa mãn \(9.k=-1\Rightarrow k=-\dfrac{1}{9}\)
\(\Rightarrow3x^2-6x=-\dfrac{1}{9}\Rightarrow x=...\)
Nghiệm xấu quá, bạn hỏi lại giáo viên coi đề chính xác không? Pt đường thẳng d là \(-x+9y-5=0\) thì có lý hơn (giải ra hoành độ tiếp điểm không bị lẻ)

Chọn D.
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số

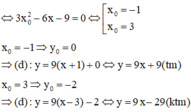

Gọi ![]() là tọa độ tiếp điểm và k là hệ số góc của tiếp tuyến.
là tọa độ tiếp điểm và k là hệ số góc của tiếp tuyến.
Theo giả thiết, ta có 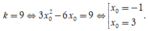
Với 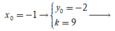 Phương trình tiếp tuyến cần tìm là: y = 9x + 7 (loại)(vì trùng với đường thẳng đã cho).
Phương trình tiếp tuyến cần tìm là: y = 9x + 7 (loại)(vì trùng với đường thẳng đã cho).
Với 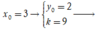 Phương trình tiếp tuyến cần tìm là: y = 9x - 25
Phương trình tiếp tuyến cần tìm là: y = 9x - 25
Chọn B.

Chọn D.
Ta có: y’ = -3x2 + 6x. Lấy điểm M(xo; yo) ∈ (C).
Tiếp tuyến tại Msong song với đường thẳng y = -9x suy ra y’(xo) = -9
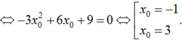
Với xo = -1 ⇒ yo = 2 ta có phương trình tiếp tuyến: y = -9x - 7
Với xo = 3 ⇒ yo = -2 ta có phương trình tiếp tuyến: y = -9x + 25
Vậy có 2 tiếp tuyến thỏa mãn.

Ta có y ' = x 2 - 4 x + 3 . Tiếp tuyến của đồ thị (C) song song với đường thẳng y = 3x - 1 nên hệ số góc của tiếp tuyến là k = 3.
Xét y' = 3 <=> x 2 - 4 x = 0
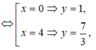
Phương trình tiếp tuyến của đồ thị tại A(0;1) có hệ số góc k = 3 là y = 3x + 1
Phương trình tiếp tuyến của đồ thị tại B(4; 7/3) có hệ số góc k = 3 là
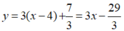
Chọn đáp án D.

Vì phương trình tiếp tuyến song song với đường thẳngy =-3x + 1nên nó có hệ số góc là -3
Do đó f ' x = 3 x 2 − 10 x = − 3 ⇔ 3 x 2 − 10 x + 3 = 0
⇔ x = 1 3 x = 3
Với x = 1 3 thì y 0 = 40 27 Vậy phương trình tiếp tuyến là: y = − 3 x − 1 3 + 40 27 = − 3 x + 67 27
Với x=3thì y 0 = - 16 Vậy phương trình tiếp tuyến là: y = -3(x- 3) – 16 = - 3x – 7
Chọn đáp án C