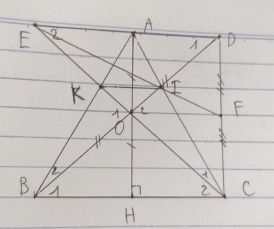
Bài 4 (3,5 điểm). Cho ∆ABC cân tại A có đường cao AH và O là trung điểm của AH. Trên tia đối của tia OB lấy điểm D sao cho OD = OB. a) Chứng minh ∆OBH = ∆ODA và AH ⊥ AD.
b) Tia CO cắt đường thẳng AD tại E. Chứng minh A là trung điểm của đoạn thẳng DE
c) AC cắt BD tại I và gọi F là trung điểm của DC. Chứng minh ba điểm E,I,F thẳng hàng