Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có f x ≥ 0 ⇔ x + 3 m ≥ 2 ⇔ x ≥ 2 - 3 m
f x ≥ 0 với mọi x ∈ [ 1 ; + ∞ ) ⇔ [ 1 ; + ∞ ) ⊂ [ 2 - 3 m ; + ∞ ) ⇔ 2 - 3 m ≤ 1 ⇔ m ≥ 1 3 .
Chọn C.
* Nếu m= 0 thì bất phương trình đã cho trở thành:
0x < 0( luôn đúng với mọi x).
* Nếu m= 1 thì bất phương trình đã cho trở thành:
0x < 1 ( luôn đúng với mọi x)
Tập tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x là {0; 1}
Để xét bất phương trình bậc nhất vô nghiệm hay luôn đúng với mọi x ta chỉ cần xét hệ số a= 0.
* Với m = 0 thì bất phương trình đã cho trở thành:
0 x ≤ 0 ( luôn đúng với mọi x) ( loại)
* Với m = -3 thì bất phương trình đã cho trở thành:
0 x ≤ 9 (luôn đúng với mọi x) ( loại)
Vậy không có giá trị nào của m để bất phương trình đã cho vô nghiệm
x - y = m ( 1 ) x 2 - x y - m - 2 = 0 ( 2 )
Từ (1), ta có y = x - m , thế vào (2) ta được phương trình:
x2 – x (x- m) – m - 2= 0 ⇔ x2 – x2 + mx –m –2 = 0
hay mx –m -2 = 0 (*) .
Hệ phương trình đã cho có nghiệm khi phương trình (*) có nghiệm ⇔ m ≠ 0 .
Chọn B.
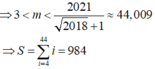
\(\Delta=\left(m+2\right)^2-4\left(3m-3\right)=m^2-8m+16=\left(m-4\right)^2\)
TH1: \(\left\{{}\begin{matrix}m=4\\-\frac{b}{2a}=\frac{m+2}{2}< 5\end{matrix}\right.\) \(\Rightarrow m=4\)
TH2: \(m\ne4\) khi đó:
\(x_1< x_2< 5\Leftrightarrow\left\{{}\begin{matrix}\left(x_1-5\right)\left(x_2-5\right)>0\\\frac{x_1+x_2}{2}< 5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-5\left(x_1+x_2\right)+25>0\\x_1+x_2< 10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3m-3-5\left(m+2\right)+25>0\\m+2< 10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2m+12>0\\m< 8\end{matrix}\right.\) \(\Rightarrow m< 6\)
\(\Rightarrow m=\left\{1;2;3;4;5\right\}\Rightarrow\sum m=15\)