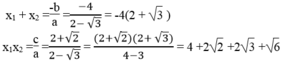Tìm tổng các hệ số của tích sau: (3-4x+x2)2014.(3+4x+x2)2015
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A\left(x\right)=\left(3-4+x^2\right)^{2004}\left(3+4x+x^2\right)^{2005}\)
Đa thức `A(x)` sau khi bỏ dấu ngoặc:
\(A\left(x\right)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\)
Với `n = 2 . 2004 + 2 . 2005 = 8018`
Ta thay `x = 1` thì \(A\left(1\right)=a_n+a_{n-1}+...+a_1+a_0\)
`=> A(1)` là tổng các hệ số của `A(x)` khi bỏ dấu ngoặc
Ta có: \(A\left(1\right)=\left(3-4.1+1^2\right)^{2004}\left(3+4.1+1^2\right)^{2005}\)
\(=0^{2004}.8^{2005}=0\)
Vậy tổng các hệ số của đa thức `A(x)` nhận được sau khi bỏ dấu ngoặc là `0`

Bài 6:
Tổng các hệ số của đa thức A(x) khi khai triển sẽ bằng với giá trị của A(x) khi x=1
=>Tổng các hệ số khi khai triển là:
\(A\left(1\right)=\left(3-4+1\right)^{2004}\cdot\left(3+1+1\right)^{2005}=0\)

Bài khó đến lớp 8 như mình còn ko bít làm thì ai làm hộ bạn đc

Ta có: ∆ ’ = 2 2 – (2 - 3 )(2 + 2 ) =4 -4 - 2 2 +2 3 + 6
= 2 3 - 2 2 + 6 >0
Phương trình 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có: