Có bao nhiêu giá trị của x thỏa mãn biểu...
Đọc tiếp
Có bao nhiêu giá trị của x thỏa mãn biểu thức: 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 10 2021
\(\Leftrightarrow3\cdot\left|2x-5\right|=12\)
\(\Leftrightarrow\left|2x-5\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=4\\2x-5=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{9}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)
26 tháng 10 2021
\(\Rightarrow3\left|5-2x\right|=12\\ \Rightarrow\left|5-2x\right|=4\Rightarrow\left[{}\begin{matrix}5-2x=4\\2x-5=4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{9}{2}\end{matrix}\right.\)
NQ
1
HT
2
C. 2 D. 
NN
5
25 tháng 10 2016
ta có : \(|x+2|\ge0\)
\(-|x+2|\le0\)
Vậy \(-|x+2|-11\le-11\)
GTNN của A = -11 khi x + 2 = 0 => x = 2
25 tháng 10 2016
A=-|x+2|-11
Vi |x+2|>hoặc =0=>-|x+2|< hoặc bang 0. =>-|x+2| lon nhat bang 0=>-|x+2|-11 lon nhat =-11
CM
4 tháng 2 2019
Đáp án D
Từ x + y = 5 4 ⇒ y = 5 4 - x vì y > 0 ⇒ 0 < x < 5 4 ⇒ S = 4 x + 1 5 - 4 x ∀ x ∈ 0 ; 5 4
Xét f ( x ) = 4 x - 1 5 - 4 x
f ' ( x ) = 0 ⇔ - 4 x 2 + 4 5 - 4 x 2 = 0 ⇒ x = 1 ∈ 0 ; 5 4
Bảng biến thiên:
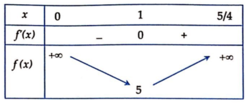
⇒ m i n S = m i n 0 ; 5 4 f ( x ) = 5 khi x = 1 y = 1 ⇒ a . b = 1 4
CM
17 tháng 4 2017
Đáp án C
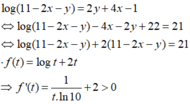
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
CM
21 tháng 11 2017
Chọn đáp án B
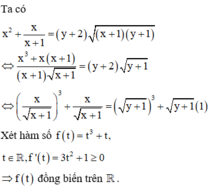
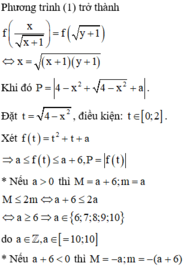
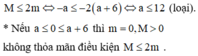
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.
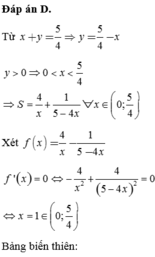
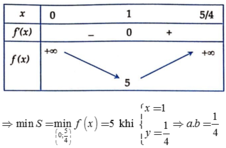
Có 2 giá trị x thỏa mãn
Có 2 giá trị x thỏa mãn !!!