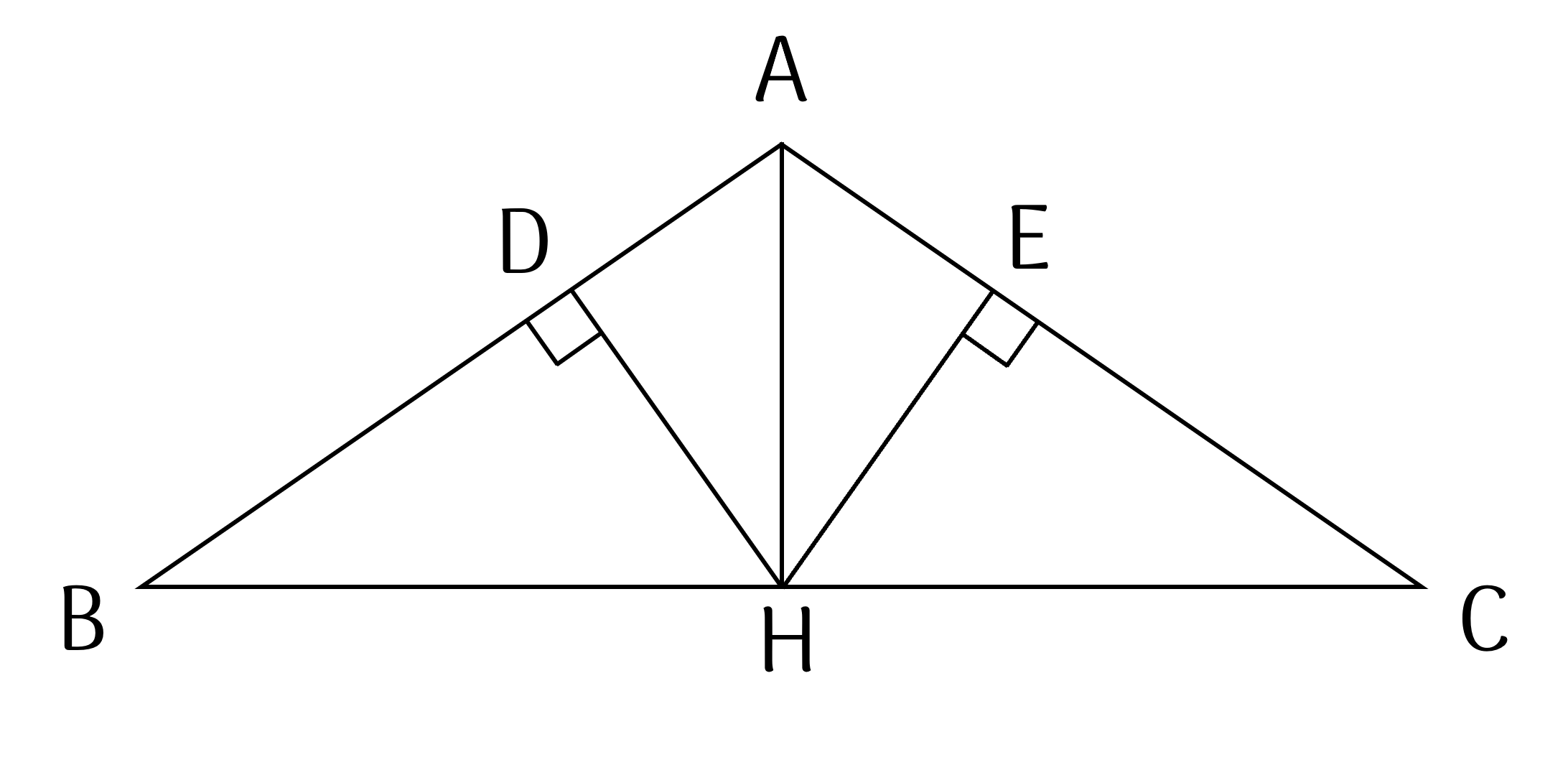
Cho \(\Delta ABC\)cân có AB = AC = 5cm, BC = 8cm. Kẻ AH là phân giác của góc BAC ( H thuộc BC )
a) Chứng minh HB = HC, từ đó tính độ dài AH
b) Gọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Chứng minh AH là đường trung trực của MN và MN // BC.
c) Không tính cụ thể hãy so sánh 2AH + BC với 2AB

a,
+) Cách 1:
Xét △ABC cân tại A (AB = AC) có: AH là phân giác BAC
=> AH là đường trung trực => ∠AHB = 90o và H là trung điểm BC => HB = HC
+) Cách 2:
Xét △BAH và △CAH
Có: AB = AC (gt)
∠BAH = ∠CAH (gt)
AH là cạnh chung
=> △BAH = △CAH (c.g.c)
=> BH = CH (2 cạnh tương ứng)
P/s: chọn 1 trong 2 cách xong làm tiếp
Ta có: HB = HC = BC : 2 = 8 : 2 = 4 (cm)
Xét △ABH vuông tại H có: AH2 + BH2 = AB2 (định lý Pytago)
=> AH2 = AB2 - BH2 = 52 - 42 = 9
=> AH = 3 (cm)
b,
+) Cách 1:
Xét △MAH vuông tại M và △NAH vuông tại N
Có: AH là cạnh chung
∠MAH = ∠NAH (gt)
=> △MAH = △NAH (cg-gn)
=> AM = AN (2 cạnh tương ứng) => A thuộc đường trung trực của MN
và MH = NH (2 cạnh tương ứng) => H thuộc đường trung trực của MN
=> AH là đường trung trực của MN
+) Cách 2: Gọi AH ∩ MN = { I }
Xét △MAH vuông tại M và △NAH vuông tại N
Có: AH là cạnh chung
∠MAH = ∠NAH (gt)
=> △MAH = △NAH (cg-gn)
=> AM = AN (2 cạnh tương ứng)
Xét △MAI và △NAI
Có: AM = AN (cmt)
∠MAI = ∠NAI (gt)
AI là cạnh chung
=> △MAI = △NAI (c.g.c)
=> MI = NI (2 cạnh tương ứng) => I là trung điểm MN
và ∠MIA = ∠NIA (2 góc tương ứng)
Mà ∠MIA + ∠NIA = 180o (2 góc kề bù)
=> ∠MIA = ∠NIA = 180o : 2 = 90o
=> AI ⊥ MN
Mà I là trung điểm MN
=> AI là đường trung trực MN
=> AH là đường trung trực MN ( AH ∩ MN = { I } )
P/s: chọn 1 trong 2 cách xong làm tiếp
Vì AM = AN (cmt) => △AMN cân tại A => ∠AMN = (180o - ∠MAN) : 2
Vì △ABC cân tại A => ∠ABC = (180o - ∠BAC) : 2
=> ∠AMN = ∠ABC
Mà 2 góc này nằm ở vị trí đồng vị
=> MN // BC (dhnb)
c, Xét △MAH vuông tại M có: AH > AM (quan hệ giữa đường xiên và đường vuông góc)
Xét △MBH vuông tại M có: BH > MB (quan hệ giữa hình chiếu và đường xiên)
Ta có: 2AH + BC = 2AH + 2BH (BH = BC : 2 => 2BH = BC)
=> 2AH + 2BH > 2AM + 2MB
=> 2AH + BC > 2(AM + MB) = 2AB