Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB=18cm, trung đoạn SI=15cm.tính thể tích của hình chóp.
Xin cảm ơn!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

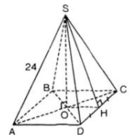
a) S.ABCD là hình chóp tứ giác đều
⇒ ABCD là hình vuông
⇒ AC = AB√2 = 20√2 (cm).
SO là chiều cao của hình chóp
⇒ O = AC ∩ BD và SO ⊥ (ABCD)
⇒ SO ⊥ AO
⇒ ΔSAO vuông tại O
⇒ SO2 + OA2 = SA2
⇒ SO2 = SA2 – OA2 = SA2 – (AC/2)2 = 242 - 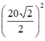 = 376
= 376
⇒ SO = √376 ≈ 19,4 (cm).
Thể tích hình chóp:
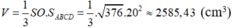
b) Gọi H là trung điểm của CD
SH2 = SD2 – DH2 = 242 – 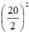 = 476
= 476
⇒ SH = √476 ≈ 21,8 (cm)
⇒ Sxq = p.d = 2.AB.SH = 2.20.√476 ≈ 872,7 (cm2 ).
Sđ = AB2 = 202 = 400 (cm2 )
⇒ Stp = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).
Lời giải:
Theo định lý Pitago:
AC=AB2+BC2−−−−−−−−−−√=102+102−−−−−−−−√=102–√AC=AB2+BC2=102+102=102 (cm)
Vì S.ABCDS.ABCD là hình chóp tứ giác đều nên OO là tâm của đáy ABCDABCD
⇒AO=AC2=52–√⇒AO=AC2=52 (cm)
SO2+AO2=SA2SO2+AO2=SA2
⇔SO2=SA2−AO2=122−(52–√)2=94⇔SO2=SA2−AO2=122−(52)2=94
⇒SO=94−−√⇒SO=94 (cm)
Thể tích hình chóp:
V=13.h.Sđáy=13.SO.AB2=10094√3V=13.h.Sđáy=13.SO.AB2=100943 (cm vuông)