cho tam giác ABC cân tại A (A nhỏ hơn 90 độ), có AD là đường phân giác. chứng minh tam giác ABD = tam giác ACD. Từ C vẽ đường thẳng vuông góc với BC tại C, đường này cắ tia BA tại E. chứng minh tam giác AEC là tam giác cân. Từ A vẽ AM vuông góc EC ( M thuộc EC). Đoạn thẳng ED cắt đoạn thẳng AC tại N. chứng minh ba điểm B,M,N thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABD vuông tại D và ΔACD vuông tại C có
AB=AC
AD chung
Do đó: ΔABD=ΔACD
=>DB=DC
=>D là trung điểm của BC
b: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
\(\widehat{EAD}=\widehat{FAD}\)(ΔABD=ΔACD)
Do đó: ΔAED=ΔAFD
=>AE=AF
=>ΔAEF cân tại A

gggggjjjk..hhhyh iuugln............................lklhuluiiiihhhhhhh ok-

a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó; ΔABD=ΔACD
a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD

a) AB // CE \(\Rightarrow\widehat{E}=\widehat{A}_2\)( hai góc so le trong )
mà \(\widehat{A}_2=\widehat{A}_1\)( gt ) nên \(\widehat{E}=\widehat{A}_2\Rightarrow\)tam giác CAE cân
Vậy AC = CE
Có AC > AB ( quan hệ giữa đường xiên và đường vuông góc )
Suy ra : CE > AB ( 1 )
Vẽ DF \(⊥\)AC , ta chứng minh được DF = DB
có DC > DF ( quan hệ giữa đường xiên và đường vuông góc ) suy ra : DC > DB
Ta có : DE2 = CE2 + DC2 ; AD2 = AB2 + DB2
Kết hợp ( 1 ) và ( 2 ) ta được : DE2 > AD2 . Do đó DE > AD ( 3 )
Từ ( 1 ), ( 2 ), ( 3 ) suy ra : CE + DC + DE > AB + DB + AD
hay chu vi tam giác ECD > chu vi tam giác ABD
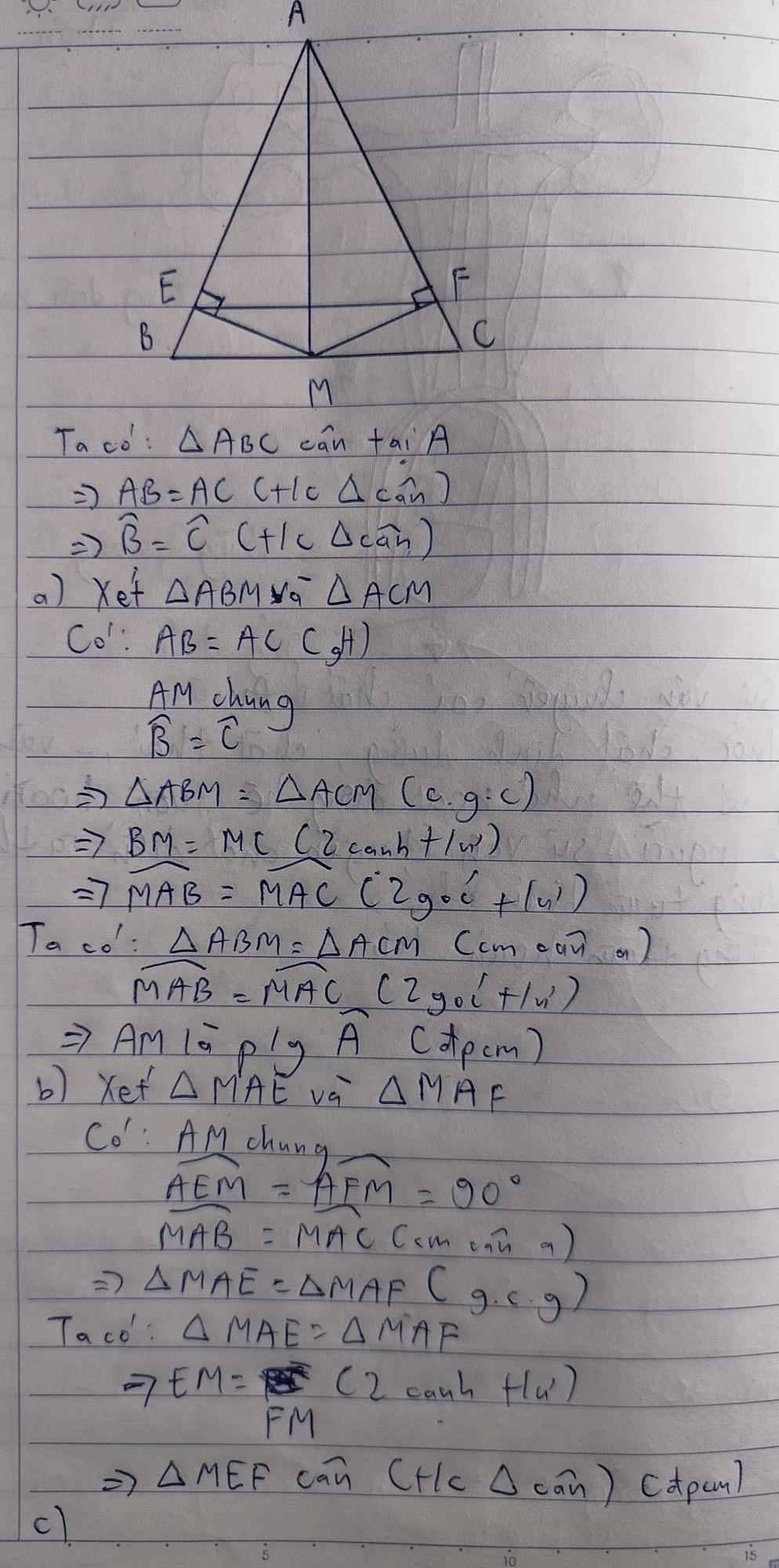
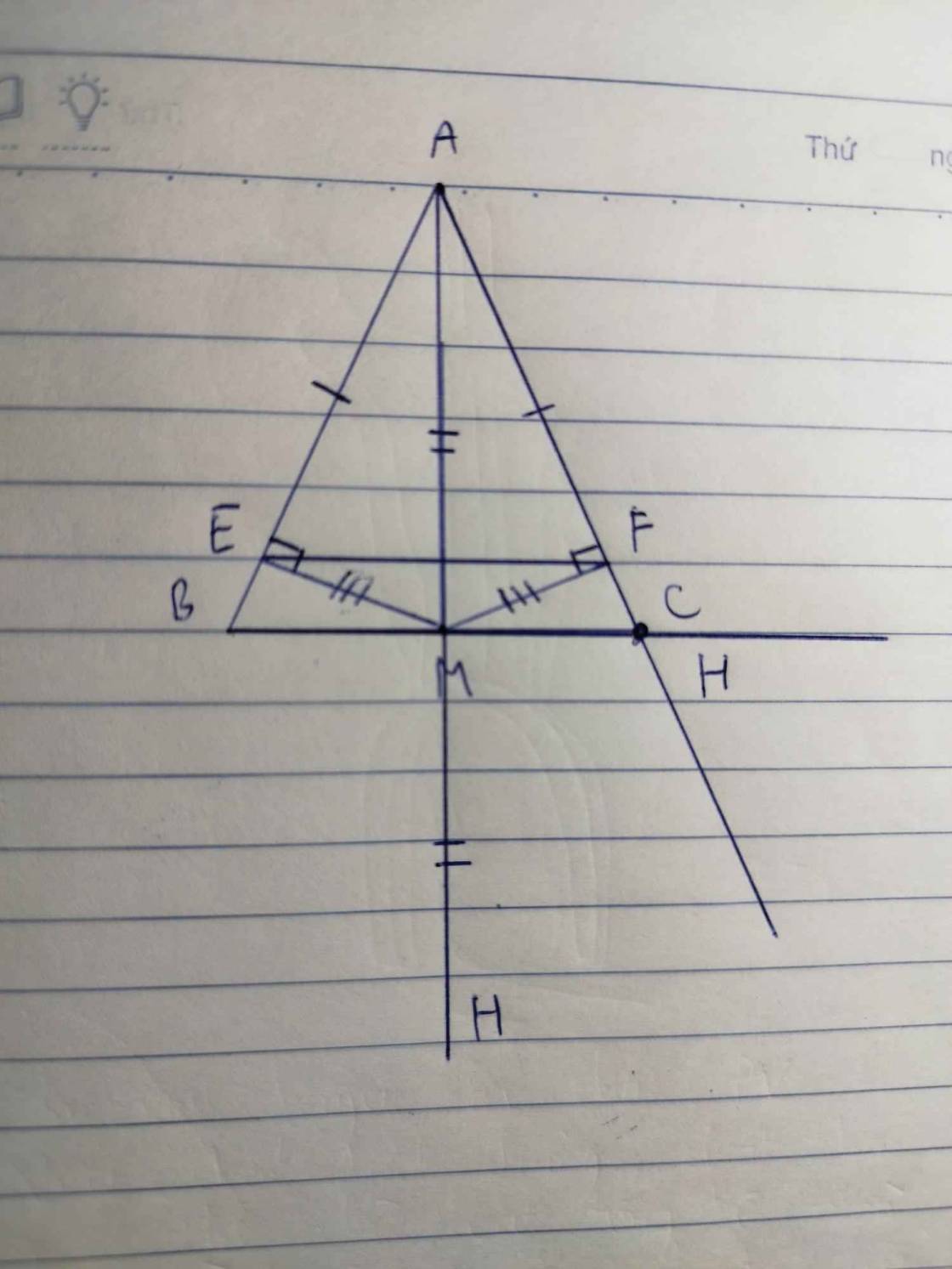
tự kẻ hình nha
a)xét tam giác ADB và tam giác ADC có
A1=A2(gt)
AD chung
AB=AC(gt)
=> tam giác ADB= tam giác ADC(cgc)
b) vì tam giác BCE vuông tại C=> BEC+EBC=90 độ=> BEC=90 độ-EBC
ta có ACB+ACE=BCE=90 độ=> ACE=90 độ-BCE
vì tam giác ABC cân A=> ABC=ACB
=> BEC=ACE=90 độ-ABC=> tam giác ACE cân A
c) xét tam giác AME và tam giác AMC có
AE=AC( tam giác ACE cân A)
AME=AMC(=90 độ)
AM chung
=> tam giác AME=tam giác AMC(ch-cgv)
=> EM=CM( hai cạnh tương ứng)
=> M là trung điểm => BM là trung tuyến
vì AB=AC mà AC=AE=> AB=AE=> A là trung điểm BE=> CA là trung tuyến
từ tam giác ABD= tam giác ACD=> BD=CD (hai cạnh tương ứng)=> D là trung điểm BC=> ED là trung tuyến
Vì ED giao AC tại N mà ED,AC, BM là trung tuyến=> BM, AC,ED giao nhau tại N=> N thuộc BM=> B,N,M thẳng hàng