em muốn hỏi câu c thui ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Trích mẫu thử :
Cho quỳ tím vào 3 mẫu thử :
+ Hóa đỏ : HCl , H2SO4
+ Hóa xanh : KOH
Cho dung dịch BaCl2 vào 2 mẫu thử làm quỳ tím hóa đỏ :
+ Chất nào xuất hiện kết tủa trắng không tan trong axit : H2SO4
Pt : \(BaCl_2+H_2SO_4\rightarrow BaSO_4+2HCl\)
Không hiện tượng : HCl
Chúc bạn học tốt
c) Trích mẫu thử :
Cho quỳ tím vào từng mẫu thử :
+ Hóa đỏ : HCl , H2SO4
+ không đổi màu : Na2SO4
Cho dung dịch BaCl2 vào 2 mẫu thử làm quỳ tím hóa đỏ :
+ Chất naò xuất hiện kết tủa trắng không tan trong axit : H2SO4
Pt : \(BaCl_2+H_2SO_4\rightarrow BaSO_4+2HCl\)
Không hiện tượng : HCl
Chúc bạn học tốt

a: \(A=\dfrac{\left(x^2-2x+5\right)\left(x-3\right)}{3\left(x-3\right)}=\dfrac{x^2-2x+5}{3}\)

a: Xét ΔEAB có \(\widehat{EBA}=\widehat{EAB}\)
nên ΔEAB cân tại E
mà EK là đường cao
nen K là trung điểm của AB
hay KA=KB
b: Xét ΔACE vuông tại C và ΔBDE vuông tại D có
EA=EB
\(\widehat{AEC}=\widehat{BED}\)
Do đó: ΔACE=ΔBDE
Suy ra: EC=ED
Ta có: AE+ED=AD
BE+CE=BC
mà AE=BE
và ED=EC
nên AD=BC

-12.(x-5)+7.(3-x)=5
-12x+12.5+7.3-7x=5
-12x-7x=5-60-21
-19x=-76
x=-76:-19
x=4
\(-12\left(x-5\right)+7\left(3-x\right)=5\)
\(\Rightarrow-12x+60+21-7x=5\)
\(\Rightarrow-12x-7x=5-21-60\)
\(\Rightarrow-19x=-76\)
\(\Rightarrow x=4\)

4:
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: AH=căn 9*16=12cm
AC=căn 12^2+16^2=20cm
HK=16*12/20=192/20=9,6cm
5:
a: Xét ΔMNP vuông tại N và ΔMHN vuông tại H có
góc M chung
=>ΔMNP đồng dạng với ΔMHN
b: NH=căn 16*9=12cm
NP=căn 16^2+12^2=20cm
HK=16*12/20=192/20=9,6cm

Với `x >= 0,x \ne 1` có:
`C=A/B=A:B=[\sqrt{x}+1]/[x+\sqrt{x}+1]:(\sqrt{x}/[x\sqrt{x}-1]+1/[\sqrt{x}-1])`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1]:[\sqrt{x}+x+\sqrt{x}+1]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1].[(\sqrt{x}-1)(x+\sqrt{x}+1)]/[x+2\sqrt{x}+1]`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1].[(\sqrt{x}-1)(x+\sqrt{x}+1)]/[(\sqrt{x}+1)^2]`
`C=[\sqrt{x}-1]/[\sqrt{x}+1]`
1.Thế \(x=4\) vào A, ta được:
\(A=\dfrac{\sqrt{4}+1}{4+\sqrt{4}+1}=\dfrac{2+1}{4+2+1}=\dfrac{3}{7}\)
2.
\(B=\dfrac{\sqrt{x}}{x\sqrt{x}-1}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}}{\sqrt{x}^3-1}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}+\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(C=\dfrac{A}{B}\)
\(C=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}:\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(C=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}.\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2}\)
\(C=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)

Câu 15
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}=\dfrac{a-b+c}{2-3+5}=\dfrac{-10.2}{4}=-2.55\)
Do đó: a=-5,1; b=-7,65; c=-12,75

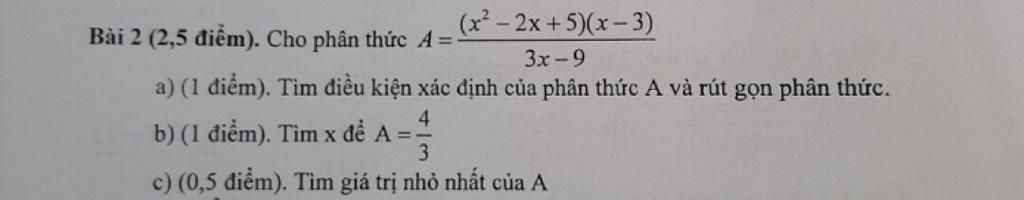


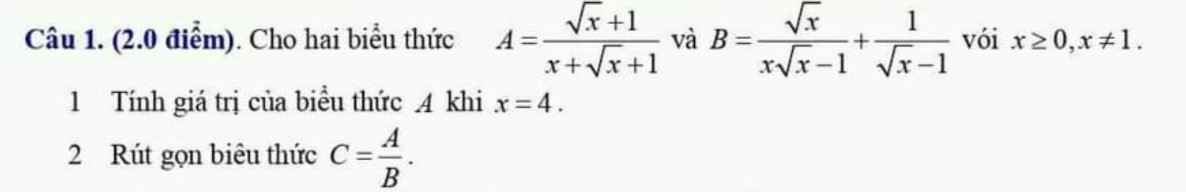
 Giúp em với ăn em cảm ơn mà giúp em mỗi câu 16 thui ạ
Giúp em với ăn em cảm ơn mà giúp em mỗi câu 16 thui ạ
c) Điện trở dây dẫn:
\(R_{dây}=\rho\cdot\dfrac{l}{S}=1,7\cdot10^{-8}\cdot\dfrac{100}{0,1\cdot10^{-6}}=17\Omega\)
Vì các điện trở và dây mắc nối tiếp nên :
\(R_m=R_1+R_2+R_3+R_{dây}=5+10+15+17=47\Omega\)
Cường độ dòng điện qua mạch lúc này:
\(I_m=\dfrac{12}{47}A\)
2+1