Cho hai đa thức P(x) = x5 - x4 và Q(x)= x4 -x3
Tìm đa thức R(x) sao cho P(x) + Q(x) + R(x) là đa thức không
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 8 2019
Ta có:
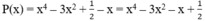
Vì : P(x) + Q(x) = x5 – 2x2 + 1
Suy ra Q(x) = x5 – 2x2 + 1– P(x).
CM
31 tháng 10 2019
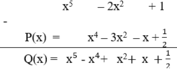
Thu gọn Q(x) = x4 + 7x2 + 1
Khi đó R(x) = Q(x) - P(x) = 4x2 + 3x + 2. Chọn A
K
19 tháng 3 2018
a) \(P\left(x\right)+Q\left(x\right)=16x^6-3x^4+5\)
\(\Rightarrow\text{}\)\(x^5-2x^4-7+x+Q\left(x\right)=16x^6-3x^4+5\)
\(\Rightarrow Q\left(x\right)=x^5-2x^4-7+x-\left(16x^6-3x^4+5\right)\)
\(\Rightarrow Q\left(x\right)=x^5-2x^4-7+x-16x^6+3x^4-5\)
\(\Rightarrow Q\left(x\right)=-16x^6+x^5+x^4+x-12\)
b) \(P\left(x\right)-R\left(x\right)=x^4\)
\(\Rightarrow x^5-2x^4-7+x-R\left(x\right)=x^4\)
\(\Rightarrow R\left(x\right)=x^5-2x^4-7+x-x^4\)
\(\Rightarrow R\left(x\right)=x^5-3x^4+x-7\)
VT
19 tháng 3 2018
a) P(x)+Q(x)=16x6−3x4+5
P(x)+Q(x)=16x6−3x4+5
⇒x5−2x4−7+x+Q(x)=16x6−3x4+5x5−2x4−7+x+Q(x)=16x6−3x4+5
⇒Q(x)=x5−2x4−7+x−(16x6−3x4+5)⇒Q(x)=x5−2x4−7+x−(16x6−3x4+5)
⇒Q(x)=x5−2x4−7+x−16x6+3x4−5⇒Q(x)=x5−2x4−7+x−16x6+3x4−5
⇒Q(x)=−16x6+x5+x4+x−12⇒Q(x)=−16x6+x5+x4+x−12
b) P(x)−R(x)=x4P(x)−R(x)=x4
⇒x5−2x4−7+x−R(x)=x4⇒x5−2x4−7+x−R(x)=x4
⇒R(x)=x5−2x4−7+x−x4⇒R(x)=x5−2x4−7+x−x4
⇒R(x)=x5−3x4+x−7
2 tháng 5 2023
`@` `\text {dnv4510}`
`A)`
`P(x)+Q(x)=`\((2x^4+3x^2-3x^2+6)+(x^4+x^3-x^2+2x+1)\)
`= 2x^4+3x^2-3x^2+6+x^4+x^3-x^2+2x+1`
`= (2x^4+x^4)+x^3+(3x^2-3x^2-x^2)+2x+(6+1)`
`= 3x^4+x^3-x^2+2x+7`
`B)`
`P(x)+M(x)=2Q(x)`
`-> M(x)= 2Q(x) - P(x)`
`2Q(x)=2(x^4+x^3-x^2+2x+1)`
`= 2x^4+2x^3-2x^2+4x+2`
`-> 2Q(x)-P(x)=(2x^4+2x^3-2x^2+4x+2)-(2x^4+3x^2-3x^2+6)`
`= 2x^4+2x^3-2x^2+4x+2-2x^4-3x^2+3x^2-6`
`= (2x^4-2x^4)+2x^3+(-2x^2-3x^2+3x^2)+4x+(2-6)`
`= 2x^3-2x^2+4x-4`
Vậy, `M(x)=2x^3-2x^2+4x-4`
`C)`
Thay `x=-4`
`M(-4)=2*(-4)^3-2*(-4)^2+4*(-4)-4`
`= 2*(-64)-2*16-16-4`
`= -128-32-16-4`
`= -180`
`->` `x=-4` không phải là nghiệm của đa thức.
CM
23 tháng 9 2019
Sắp xếp lại các hạng tử của Q(x) ta có :
Q(x) = –3x5 + x4 + 3x3 – 2x + 6.
Đặt và thực hiện các phép tính P(x) – Q(x) và Q(x) – P(x), ta có
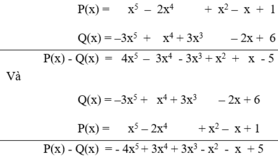
Nhận xét : Các hệ số tương ứng của P(x) – Q(x) và Q(x) - P(x) đối nhau.
Chú ý : Ta gọi hai đa thức có các hệ số tương ứng đối nhau là đa thức đối nhau.
TL
1
18 tháng 6 2020
Theo bài ra ta có : \(P\left(x\right)+Q\left(x\right)+R\left(x\right)=0\)
\(\Leftrightarrow x^5-x^4+x^4-x^3+R\left(x\right)=0\)
\(\Leftrightarrow x^5-x^3=R\left(x\right)\)
Từ những Đk trên suy ra : \(P\left(x\right)+Q\left(x\right)+R\left(x\right)=x^5-x^4+x^4-x^3+x^5-x^3=0\)
\(\Leftrightarrow2x^5-2x^3=0\)
Vậy P(x) + Q(x) + R(x) là đa thức.
Ta có : \(P\left(x\right)+Q\left(x\right)+R\left(x\right)\)
\(\Leftrightarrow\left(x^5-x^4\right)+\left(x^4-x^3\right)+R\left(x\right)\)
\(\Leftrightarrow x^5-x^4+x^4-x^3+R\left(x\right)\)
\(\Leftrightarrow x^5-x^3+R\left(x\right)\)Đặt \(x^5-x^3+R\left(x\right)=0\)
\(\Leftrightarrow R\left(x\right)=-x^5+x^3\) => Đa thức chứ còn j nữa =))