Giúp mình câu 12 với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 12 2021
Câu 1:
\(a,B=\dfrac{2\cdot3-1}{9-4}=\dfrac{5}{5}=1\\ b,A=\dfrac{x-2\sqrt{x}+x+2\sqrt{x}-2x+\sqrt{x}+5}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+5}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ b,\dfrac{A}{B}=\dfrac{\sqrt{x}+5}{x-4}\cdot\dfrac{x-4}{2\sqrt{x}-1}=\dfrac{\sqrt{x}+5}{2\sqrt{x}-1}< 0\\ \Leftrightarrow2\sqrt{x}-1< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow\sqrt{x}< \dfrac{1}{2}\Leftrightarrow0\le x< \dfrac{1}{4}\)
26 tháng 12 2021
1 a) Với \(a\ge0\) và \(a\ne4\) ta có
\(A=\dfrac{\sqrt{x}}{\sqrt{x}+2}-\dfrac{\sqrt{x}}{2-\sqrt{x}}-\dfrac{2x-2\sqrt{x}-5}{x-4},B=\dfrac{2\sqrt{x}-1}{x-4}\)
a)
A=\(\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{\sqrt{x}}{-\left(\sqrt{x}-2\right)}-\dfrac{2x-2\sqrt{x}-5}{x-4}\)
A=\(\dfrac{\sqrt{x}+\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{2x-2\sqrt{x}-5}{x-4}\)
A=\(\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)+\sqrt{x}\left(\sqrt{x}+2\right)}{x-4}-\dfrac{2x-2\sqrt{x}-5}{x-4}\)
A=\(\dfrac{x-2\sqrt{x}+x+2\sqrt{x}}{x-4}-\dfrac{2x-2\sqrt{x}-5}{x-4}\)=\(\dfrac{2x}{x-4}-\dfrac{2x-2\sqrt{x}-5}{x-4}\)=\(\dfrac{2x-2x+2\sqrt{x}+5}{x-4}\)
A=\(\dfrac{2\sqrt{x}+5}{x-4}\)
Gía Trị Của B Khi x=9 Là ;
B=\(\dfrac{2\sqrt{9}-1}{9-4}=\dfrac{6-1}{5}=\dfrac{5}{5}=1\)
:)) câu c ko chắc :V
để \(\dfrac{A}{B}< 0\)(=)\(\dfrac{2\sqrt{x}+5}{x-4}:\dfrac{2\sqrt{x}-1}{x-4}\left(=\right)\dfrac{2\sqrt{x}+4}{x-4}\cdot\dfrac{x-4}{2\sqrt[]{x}-1}\left(=\right)\dfrac{\left(2\sqrt{x}+4\right)\left(x-4\right)}{\left(x-4\right)\left(2\sqrt{x}-1\right)}\)(=)\(\dfrac{2\sqrt{x}+4}{2\sqrt{x}-1}\)<0(=) bí :V
DT
Đỗ Thanh Hải
CTVVIP
13 tháng 8 2021
1 would help
2 had
3 wouldn't do
4 had
5 could visit
6 would come
7 would come
8 were
8 were
14 tháng 3 2022
Câu 1:
a: \(\Leftrightarrow6x^2-2x=6x^2-13\)
=>-2x=-13
hay x=13/2
b: \(\Leftrightarrow2x-2x-1=x-6x\)
=>-5x=-1
hay x=1/5
c: \(\Leftrightarrow\left(x+1\right)^2-\left(x-1\right)^2=x^2+3\)
\(\Leftrightarrow x^2+3=x^2+2x+1-x^2+2x-1=4x\)
\(\Leftrightarrow x^2-4x+3=0\)
=>(x-1)(x-3)=0
=>x=3(nhận) hoặc x=1(loại)
14 tháng 3 2022
Bài 4:
\(\left(x^2+x+4\right)^2+8x\left(x^2+x+4\right)+16x^2=0\)
\(\Leftrightarrow\left(x^2+x+4\right)^2+2.4x\left(x^2+x+4\right)+\left(4x\right)^2=0\)
\(\Leftrightarrow\left(x^2+x+4+4x\right)^2=0\)
\(\Leftrightarrow\left(x^2+5x+4\right)^2=0\)
\(\Leftrightarrow\left(x^2+4x+x+4\right)^2=0\)
\(\Leftrightarrow\left[x\left(x+4\right)+x+4\right]^2=0\)
\(\Leftrightarrow\left(x+1\right)^2.\left(x+4\right)^2=0\)
\(\Leftrightarrow\left(x+1\right)^2=0\) hay \(\left(x+4\right)^2=0\)
\(\Leftrightarrow x=-1\) hay \(x=-4\)
-Vậy \(S=\left\{-1;-4\right\}\)
NT
1
HL
14 tháng 11 2021
câu 3 : kq 2 phần 3
câu 4 : kq -1
câu 5 : kq -8 phần 3
câu 6 : kq 4 phần 3
câu 7 : kq -3
câu 9 : x = 1 phần 2
câu 10 : kq x =13 phần 12
câu 12 : 2 mũ 3 phần 3 mũ 3 = 8 phần 27
câu 13 : câu D nha
câu 10 ; 12 mình ko trắc lắm đâu nha
còn câu 8 mình ko rỏ mình sẻ tính lại sau
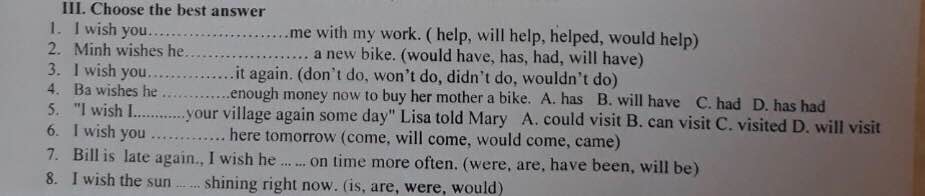
Giúp mình phiếu học tập 3 - câu 1,2 vs ạ
NV
0
Jdifriuurir8r
A