cho các số thực không âm cmr
(a+b+c) mũ 3 >= a mũ 3 + b mũ 3 + c mũ 3 + 24abc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(A=\dfrac{2}{3}x^2y\cdot\dfrac{3}{4}x^4y^3=\dfrac{1}{2}x^6y^4\)
\(B=\dfrac{-1}{2}xy^2\cdot4x^5y^2=-2x^6y^4\)
b: \(C=A-B=\dfrac{-3}{2}x^6y^4\)
Bậc là 10
c: A-B nhận được giá trị âm với mọi x,y

a, \(A=\left(-\dfrac{2}{3}x^2y\right)\left(-\dfrac{3}{5}x^2y^3\right)=\dfrac{2}{5}x^4y^4\)
b,Thay x = -1 ; y = 2 ta được \(\dfrac{2^5}{5}=\dfrac{32}{5}\)
c, \(B=\dfrac{2}{5}x^4y^4-x^4y^4-3=-\dfrac{3}{5}x^4y^3-3< 0\)
Vậy B luôn nhận gtr âm

a: \(a^3-a=a\left(a-1\right)\left(a+1\right)\)
Vì a;a-1;a+1 là ba số nguyên liên tiếp
nên \(a\left(a-1\right)\left(a+1\right)⋮3!\)
hay \(a^3-a⋮6\)

A) a^3 là cả âm lẫn dương bởi vì còn tùy thuộc vào dk của a>0 hoặc a<0
B) a^3 +a = a(a^2+1) , Ta có a^2 +1 >0 là số dương, tích này muốn dương thì a> 0, số âm thì a<0
C) Ta có a^6, a^4,a^2 là các số mũ chẵn => tổng 3 số là số dương
Thick mình
\(a,a>0\Rightarrow a^3>0\)
\(a<0\Rightarrow a^3<0\)
\(a=0\Rightarrow a^{3=0}\)
Cau b so sanh voi 1
cau c cm \(\ge\)0

Bài này cần dùng một ít kiến thức của lớp 8, bạn có thể tìm hiểu thêm.
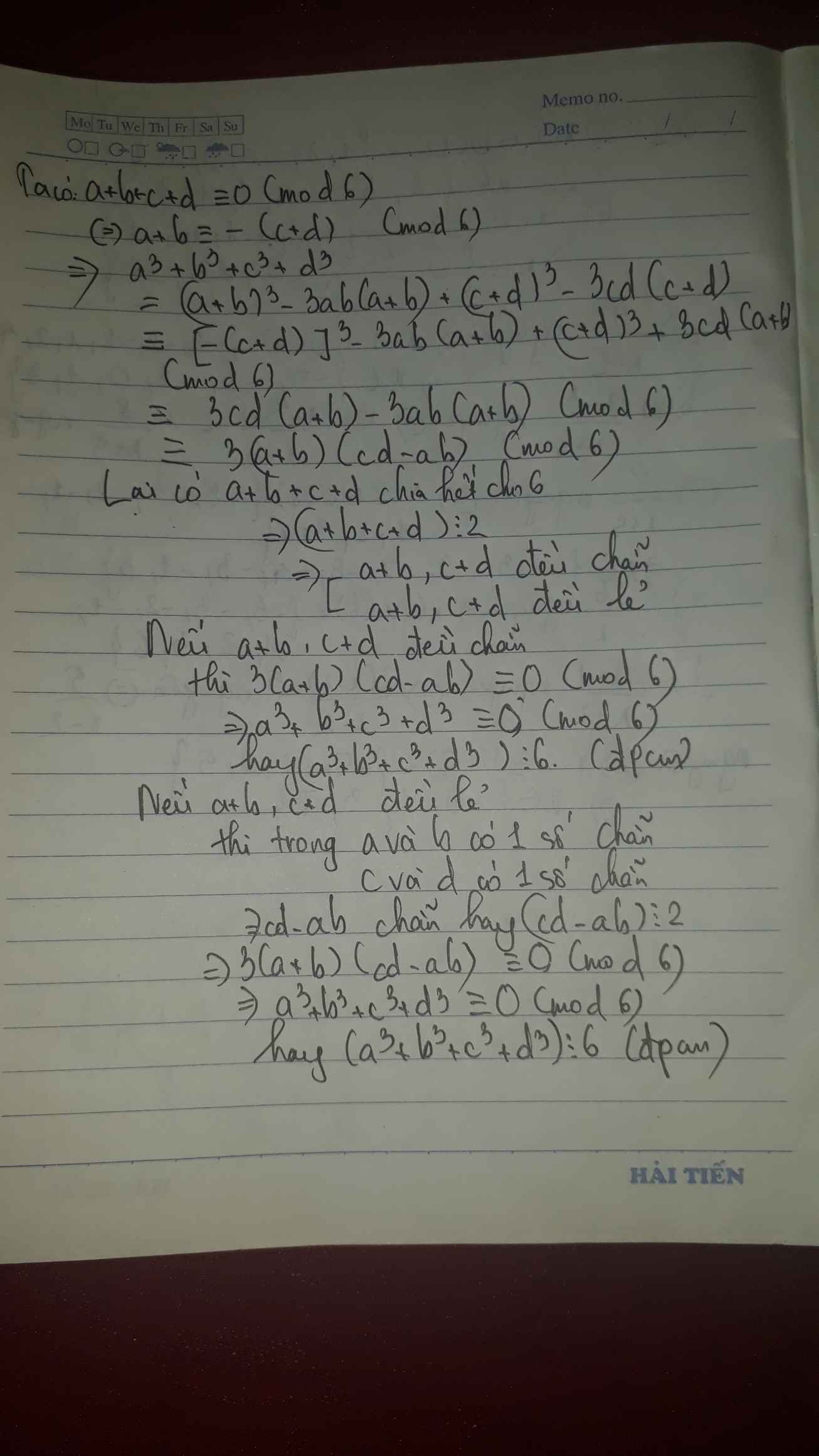

\(a,3^6:3^5=3^{6-5}=3\\ b,5^7:5^5=5^{7-5}=5^2=25\\ c,14^5:2^3:7^4=\left(2^5:2^3\right)\cdot\left(7^5:7^4\right)=2^2\cdot7=28\\ d,5^4-2\cdot5^3=5^3\left(5-2\right)=3\cdot5^3=375\)
a) 3^6 : 3^5 = 729 : 243 = 3
b) 5^7 : 5^5 = 78125 : 3125 = 25
c) 14^5 : 2^3 : 7^4 = 537824 : 8 : 2401 = 89
d) 5^4 - 2 * 5^3 = 625 - 2 * 125 = 625 - 250 = 375
Ta có : \(\left(a+b+c\right)^3=a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(a+c\right)\)
Như vậy, cần chứng minh :
\(\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8abc\)
Áp dụng BĐT Cô-si,ta có :
\(a+b\ge2\sqrt{ab};b+c\ge2\sqrt{bc};a+c\ge2\sqrt{ac}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\sqrt{a^2b^2c^2}=8abc\)
Vậy ta có điều phải chứng minh.
Dấu"=" xảy ra khi a = b = c