cho tan α +cotα =m với | m| ≥2. tính tan α - cotα
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Ta có tan α – cotα = 1

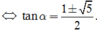
Do ![]() suy ra tanα < 0 nên
suy ra tanα < 0 nên
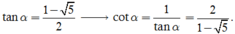
Thay
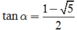 và
và 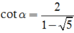
vào P ta được
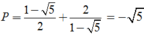

2tan a-cot a=1
=>2tana-1/tan a=1
=>\(\dfrac{2tan^2a-1}{tana}=1\)
=>2tan^2a-tana-1=0
=>(tan a-1)(2tana+1)=0
=>tan a=-1/2 hoặc tan a=1
\(P=\dfrac{tan\left(-a\right)+2\cdot cota}{3\cdot tan\left(\dfrac{pi}{2}+a\right)}=\dfrac{-tana+2\cdot cota}{-3\cdot cota}\)
TH1: tan a=-1/2
\(P=\dfrac{\dfrac{1}{2}+2\cdot\left(-2\right)}{-3\cdot\left(-2\right)}=-\dfrac{7}{2}:6=-\dfrac{7}{12}\)
TH2: tan a=1
=>cot a=1
\(P=\dfrac{-1+2}{-3}=\dfrac{1}{-3}=-\dfrac{1}{3}\)
Ta có :
\(2tan\alpha-cot\alpha=1\)
\(\Leftrightarrow2tan\alpha-\dfrac{1}{tan\alpha}=1\)
\(\Leftrightarrow2tan\alpha-\dfrac{1}{tan\alpha}-1=0\)
\(\Leftrightarrow\dfrac{2tan^2\alpha-tan\alpha-1}{tan\alpha}=0\left(tan\alpha\ne0\right)\)
\(\Leftrightarrow2tan^2\alpha-tan\alpha-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tan\alpha=1\\tan\alpha=-\dfrac{1}{2}\end{matrix}\right.\)
\(P=\dfrac{tan\left(8\pi-\alpha\right)+2cot\left(\pi+\alpha\right)}{3tan\left(\dfrac{3\pi}{2}+\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{tan\left(4.2\pi-\alpha\right)+2cot\alpha}{3tan\left(2\pi-\dfrac{\pi}{2}+\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{tan\left(-\alpha\right)+2cot\alpha}{3tan\left[-\left(\dfrac{\pi}{2}-\alpha\right)\right]}\)
\(\Leftrightarrow P=\dfrac{-tan\alpha+2cot\alpha}{-3tan\left(\dfrac{\pi}{2}-\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{-tan\alpha+2cot\alpha}{-3cot\alpha}\)
- Với \(tan\alpha=1\Rightarrow cot\alpha=1\)
\(\Leftrightarrow P=\dfrac{-1+2.1}{-3.1}=-\dfrac{1}{3}\)
- Với \(tan\alpha=-\dfrac{1}{2}\Rightarrow cot\alpha=-2\)
\(\Leftrightarrow P=\dfrac{\dfrac{1}{2}+2.\left(-2\right)}{-3.\left(-2\right)}=\dfrac{-\dfrac{7}{2}}{6}=-\dfrac{7}{12}\)

Trên đường tròn lượng giác,từ A(1,0) vẽ tiếp tuyến t’At với đường tròn lượng giác.
Từ B(0,1) vẽ tiếp tuyến s’Bs với đường tròn lượng giác .
Cho cung lượng giác AM có số đo α (α ≠ π/2 + kπ ). Gọi T là giao điểm của OM với trục t’At.
Gọi S là giao điểm của OM và trục s’Bs.
Khi β = α + kπ thì điểm cuối của góc β sẽ trùng với điểm T trên trục tan. Do đó
tan(α + kπ) = tanα.
Khi β = α + kπ thì điểm cuối của góc β sẽ trùng với điểm S trên trục cot. Do đó
cot(α + kπ) = cotα.

Vì \(\dfrac{\pi}{2}< \alpha< \pi\) \(\Rightarrow\) cos \(\alpha\) < 0
\(\Rightarrow\) cos \(\alpha\) = \(-\sqrt{1-sin^2\alpha}\) = \(-\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow\) tan \(\alpha\) = \(\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\sqrt{2}}{4}\)
\(\Rightarrow\) cot \(\alpha\) = \(\dfrac{1}{tan\alpha}\) = \(-2\sqrt{2}\)
Chúc bn học tốt!

Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có: sin 2 α + cos 2 α = 1
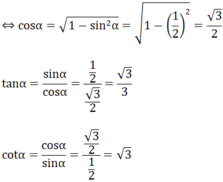
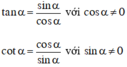
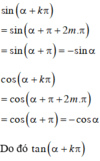
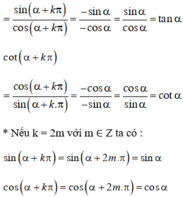
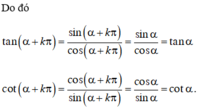
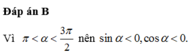
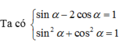
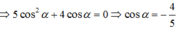
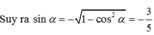
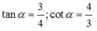

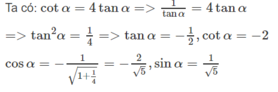
\(\left(tana+cota\right)^2=m^2\)
\(\Leftrightarrow tan^2a+cot^2a+2=m^2\)
\(\Leftrightarrow tan^2a+cot^2a-2.tana.cota=m^2-4\)
\(\Leftrightarrow\left(tana-cota\right)^2=m^2-4\)
\(\Rightarrow tana-cota=\pm\sqrt{m^2-4}\)