Cho đường thẳng d: 3x+ 4y – 10 = 0, điểm M(1; 2). Tìm toạ độ điểm H hình chiếu của M trên d và điểm M' đối xứng với M qua d.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
Gọi d' là đường thẳng qua M và vuông góc d \(\Rightarrow\) d' nhận (4;-3) là 1 vtpt
Phương trình d':
\(4\left(x-2\right)-3\left(y-1\right)=0\Leftrightarrow4x-3y-5=0\)
Gọi N là giao điểm của d và d' \(\Rightarrow\)tọa độ N thỏa mãn:
\(\left\{{}\begin{matrix}3x+4y+10=0\\4x-3y-5=0\end{matrix}\right.\) \(\Rightarrow N\left(-\dfrac{2}{5};-\dfrac{11}{5}\right)\)
M' là ảnh của M qua phép đối xứng trục d \(\Leftrightarrow\) N là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_N-x_M=-\dfrac{14}{5}\\y_{M'}=2y_N-y_M=-\dfrac{27}{5}\end{matrix}\right.\)
\(\Rightarrow M'\left(-\dfrac{14}{5};-\dfrac{27}{5}\right)\)
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
Lời giải:
Gọi $M'(a,b)$ là ảnh của $M$ đối xứng qua $d$
$\overrightarrow{MM'}=(a-2,b-1)$
Vì $\overrightarrow{MM'}\perp \overrightarrow{u_d}$ nên:
$\frac{a-2}{2}=\frac{b-1}{1}\Leftrightarrow a-2=2(b-1)(1)$
$I$ là trung điểm $MM'$. $x_I=\frac{2+a}{2}; y_I=\frac{b+1}{2}$
$3.\frac{2+a}{2}+4.\frac{b+1}{2}+10=0$
$\Leftrightarrow 3a+4b+30=0(2)$
Từ $(1);(2)\Rightarrow a=-6;b=-3$
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 7 2021
Đường thẳng song song d nên nhận (3;-4) là 1 vtpt
Phương trình:
\(3\left(x-2\right)-4\left(y-1\right)=0\Leftrightarrow3x-4y-2=0\)
TT
1
AH
Akai Haruma
Giáo viên
14 tháng 3 2018
Lời giải:
Khoảng cách từ điểm $N$ đến $d$ bạn chỉ cần áp dụng công thức thôi:
\(d(N,d)=\frac{|3.2+4(-1)-10|}{\sqrt{3^2+4^2}}=\frac{8}{5}\)
Ghi nhớ: Đường thẳng \( ax+by+c=0\) thì khoảng cách từ \(M(x_0;y_0)\) đến đường thẳng đã cho là:
\(d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
CM
21 tháng 5 2019
Lấy điểm M( x0; 1-2x0) nằm trên d.
Từ giả thiết ta có:
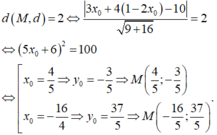
Chọn C.
25 tháng 1
a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)
CM
30 tháng 11 2018
Do 2 đường thẳng d và d’ vuông góc với nhau nên d có véc tơ chỉ phương
.
Mà d đi qua điểm M( -2; 3) nên d có phương trình tham số là:
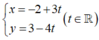
Chọn B.
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 9 2020
Do I thuộc d nên tọa độ có dạng: \(I\left(3a-8;-a\right)\)
(C) qua A nên \(IA=R\)
\(\overrightarrow{AI}=\left(3a-6;-a-1\right)\Rightarrow R=\sqrt{10a^2-34a+37}\)
(C) tiếp xúc d' nên:
\(R=d\left(I;d'\right)\Leftrightarrow\sqrt{10a^2-34a+37}=\frac{\left|3\left(3a-8\right)+4a+10\right|}{\sqrt{3^2+\left(-4\right)^2}}\)
\(\Leftrightarrow5\sqrt{10a^2-34a+37}=\left|13a-14\right|\)
\(\Leftrightarrow25\left(10a^2-34a+37\right)=\left(13a-14\right)^2\)
\(\Leftrightarrow81a^2-486a+729=0\)
\(\Leftrightarrow a=3\Rightarrow\left\{{}\begin{matrix}I\left(1;-3\right)\\R=5\end{matrix}\right.\)
Phương trình: \(\left(x-1\right)^2+\left(y+3\right)^2=25\)
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 4 2019
Gọi M là giao điểm của \(d_1\) và \(d_2\Rightarrow\) toạ độ M là nghiệm của hệ:
\(\left\{{}\begin{matrix}3x-2y+5=0\\2x+4y-7=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{3}{8};\frac{31}{16}\right)\)
Do \(d//d_3\Rightarrow d\) nhận \(\overrightarrow{n_d}=\left(3;4\right)\) là 1 vtpt
Phương trình d:
\(3\left(x+\frac{3}{8}\right)+4\left(y-\frac{31}{16}\right)=0\Leftrightarrow24x+32y-53=0\)
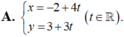
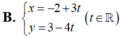
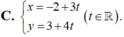
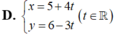
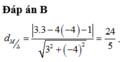
Pt đường thẳng d' qua M và vuông góc d:
\(4\left(x-1\right)-3\left(y-2\right)=0\Leftrightarrow4x-3y+2=0\)
H là giao điểm d và d' nên tọa độ thỏa: \(\left\{{}\begin{matrix}3x+4y-10=0\\4x-3y+2=0\end{matrix}\right.\) \(\Rightarrow H\left(\frac{22}{25};\frac{46}{25}\right)\)
M' đối xứng M qua d \(\Leftrightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=\frac{19}{25}\\y_{M'}=2y_H-y_M=\frac{42}{25}\end{matrix}\right.\) \(\Rightarrow M'\left(\frac{19}{25};\frac{42}{25}\right)\)