cho A = \(\frac{-\left(\sqrt{7-4\sqrt{3}}+\sqrt{7+4\sqrt{3}}\right)}{\sqrt{7-4\sqrt{3}}-\sqrt{7+4\sqrt{3}}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 2 2022
3: \(=\left(4+\sqrt{15}\right)\cdot\left(\sqrt{5}-\sqrt{3}\right)\cdot\sqrt{8-2\sqrt{15}}\)
\(=\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\)
\(=32-8\sqrt{15}+8\sqrt{15}-30=2\)
4: \(=\dfrac{\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{7}-1-\sqrt{7}-1}{\sqrt{2}}=-\sqrt{2}\)
5: \(=\dfrac{\sqrt{23-8\sqrt{7}}}{3}+\dfrac{\sqrt{23+8\sqrt{7}}}{3}\)
\(=\dfrac{4-\sqrt{7}+4+\sqrt{7}}{3}=\dfrac{8}{3}\)
AH
Akai Haruma
Giáo viên
30 tháng 9 2023
a.
$A=\sqrt{2-\sqrt{3}}+\sqrt{2+\sqrt{3}}$
$A\sqrt{2}=\sqrt{4-2\sqrt{3}}+\sqrt{4+2\sqrt{3}}$
$A\sqrt{2}=\sqrt{(\sqrt{3}-1)^2}+\sqrt{(\sqrt{3}+1)^2}$
$=|\sqrt{3}-1|+|\sqrt{3}+1|=\sqrt{3}-1+\sqrt{3}+1=2\sqrt{3}$
$\Rightarrow A=2\sqrt{3}: \sqrt{2}=\sqrt{6}$
---------------------
$B=\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}$
$B\sqrt{2}=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}$
$B\sqrt{2}=\sqrt{(\sqrt{7}-1)^2}-\sqrt{(\sqrt{7}+1)^2}$
$=|\sqrt{7}-1|-|\sqrt{7}+1|=\sqrt{7}-1-(\sqrt{7}+1)=-2$
$\Rightarrow B=-2:\sqrt{2}=-\sqrt{2}$
H
30 tháng 9 2023
\(a,\sqrt{2-\sqrt{3}}+\sqrt{2+\sqrt{3}}\)
\(A-\sqrt{2}=\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)\cdot\sqrt{2}\\ =\sqrt{2-\sqrt{3}}\cdot\sqrt{2}-\sqrt{2+\sqrt{3}}\cdot\sqrt{2}\\ =\sqrt{\left(2-\sqrt{3}\right)\cdot2}-\sqrt{\left(2+\sqrt{3}\right)\cdot2}\\ =\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\\ =\sqrt{3-2\sqrt{3}+1}-\sqrt{3+2\sqrt{3}+1}\\ =\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\\ =\left|\sqrt{3}-1\right|-\left|\sqrt{3}+1\right|\\ =\sqrt{3}-1-\sqrt{3}-1\\ =-2\)
Ta có :
\(A-\sqrt{2}=-2\\ \Leftrightarrow A=\dfrac{-2}{\sqrt{2}}=\dfrac{-\left(\sqrt{2}\right)^2}{\sqrt{2}}=-\sqrt{2}\)
__
C làm giống câu a, nhé.
__
\(\sqrt{\left(2\sqrt{5}+1\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}\\ =\left|2\sqrt{5}+1\right|-\left|\sqrt{5}-2\right|\\ =2\sqrt{5}+1-\sqrt{5}+2\\ =3+\sqrt{5}\)
__
\(\sqrt{52-16\sqrt{3}}+\sqrt{\left(4\sqrt{3}-7\right)^2}\\ =\sqrt{48-2\cdot4\cdot\sqrt{3}\cdot2+4}+\left|4\sqrt{3}-7\right|\\ =\sqrt{\left(4\sqrt{3}\right)^2-2\cdot4\cdot\sqrt{3}\cdot2+2^2}+4\sqrt{3}-7\\ =\sqrt{\left(4\sqrt{3}-2\right)^2}+4\sqrt{3}-7\\ =4\sqrt{3}-2+4\sqrt{3}-7\\ =8\sqrt{3}-9\)
12 tháng 8 2020
a) Ta có: \(A=\sqrt{8-2\sqrt{15}}\cdot\left(\sqrt{3}+\sqrt{5}\right)-\left(\sqrt{45}-\sqrt{20}\right)\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot\sqrt{3}+3}\cdot\left(\sqrt{5}+\sqrt{3}\right)-\sqrt{5}\left(\sqrt{9}-\sqrt{4}\right)\)
\(=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\cdot\left(\sqrt{5}+\sqrt{3}\right)-\sqrt{5}\)
\(=\left|\sqrt{5}-\sqrt{3}\right|\cdot\left(\sqrt{5}+\sqrt{3}\right)-\sqrt{5}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\cdot\left(\sqrt{5}+\sqrt{3}\right)-\sqrt{5}\)(Vì \(\sqrt{5}>\sqrt{3}\))
\(=5-3-\sqrt{5}\)
\(=2-\sqrt{5}\)
b) Ta có: \(B=\left(\frac{\sqrt{21}-\sqrt{3}}{\sqrt{7}-1}-\frac{\sqrt{15}-\sqrt{3}}{1-\sqrt{5}}\right)\left(\frac{1}{2}\sqrt{6}-\sqrt{\frac{3}{2}}+3\sqrt{\frac{2}{3}}\right)\)
\(=\left(\frac{\sqrt{3}\left(\sqrt{7}-1\right)}{\sqrt{7}-1}+\frac{\sqrt{3}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}\right)\left(\sqrt{\frac{3}{2}}-\sqrt{\frac{3}{2}}+\sqrt{6}\right)\)
\(=\sqrt{3}+\sqrt{3}+\sqrt{6}\)
\(=2\sqrt{3}+\sqrt{6}\)
c) Ta có: \(C=2\sqrt{3}+\sqrt{7-4\sqrt{3}}+\left(\sqrt{\frac{1}{3}}-\sqrt{\frac{4}{3}}+\sqrt{3}\right):\sqrt{3}\)
\(=2\sqrt{3}+\sqrt{4-2\cdot2\cdot\sqrt{3}+3}+\sqrt{\frac{1}{3}:3}-\sqrt{\frac{4}{3}:3}+\sqrt{3:3}\)
\(=2\sqrt{3}+\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{\frac{1}{9}}-\sqrt{\frac{4}{9}}+\sqrt{1}\)
\(=2\sqrt{3}+\left|2-\sqrt{3}\right|+\frac{1}{3}-\frac{2}{3}+1\)
\(=2\sqrt{3}+2-\sqrt{3}+\frac{2}{3}\)(Vì \(2>\sqrt{3}\))
\(=\sqrt{3}+\frac{8}{3}\)
d) Ta có: \(D=\left(\frac{5+\sqrt{5}}{5-\sqrt{5}}+\frac{5-\sqrt{5}}{5+\sqrt{5}}\right):\frac{1}{\sqrt{7-4\sqrt{3}}}\)
\(=\left(\frac{\left(5+\sqrt{5}\right)^2+\left(5-\sqrt{5}\right)^2}{\left(5-\sqrt{5}\right)\left(5+\sqrt{5}\right)}\right)\cdot\sqrt{4-2\cdot2\cdot\sqrt{3}+3}\)
\(=\frac{25+10\sqrt{5}+5+25-10\sqrt{5}+5}{25-5}\cdot\sqrt{\left(2-\sqrt{3}\right)^2}\)
\(=\frac{60}{20}\cdot\left|2-\sqrt{3}\right|\)
\(=3\cdot\left(2-\sqrt{3}\right)\)(Vì \(2>\sqrt{3}\))
\(=6-3\sqrt{3}\)
AH
Akai Haruma
Giáo viên
26 tháng 6 2021
\(A=\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}=\sqrt{3+1+2\sqrt{3.1}}-\sqrt{3+1-2\sqrt{3.1}}\)
\(=\sqrt{(\sqrt{3}+1)^2}-\sqrt{(\sqrt{3}-1)^2}=|\sqrt{3}+1|-|\sqrt{3}-1|=2\)
\(B=\sqrt{4+5-2\sqrt{4.5}}+\sqrt{4+5+2\sqrt{4.5}}=\sqrt{(\sqrt{4}-\sqrt{5})^2}+\sqrt{(\sqrt{4}+\sqrt{5})^2}\)
\(=|\sqrt{4}-\sqrt{5}|+|\sqrt{4}+\sqrt{5}|=2\sqrt{5}\)
AH
Akai Haruma
Giáo viên
26 tháng 6 2021
\(C\sqrt{2}=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}=\sqrt{7+1-2\sqrt{7.1}}-\sqrt{7+1+2\sqrt{7.1}}\)
\(=\sqrt{(\sqrt{7}-1)^2}-\sqrt{(\sqrt{7}+1)^2}\)
\(=|\sqrt{7}-1|-|\sqrt{7}+1|=-2\Rightarrow C=-\sqrt{2}\)
----------------------------
\(7+4\sqrt{3}=(2+\sqrt{3})^2\Rightarrow 10\sqrt{7+4\sqrt{3}}=10(2+\sqrt{3})\)
\(\Rightarrow \sqrt{48-10\sqrt{7+4\sqrt{3}}}=\sqrt{28-10\sqrt{3}}=\sqrt{(5-\sqrt{3})^2}=5-\sqrt{3}\)
\(\Rightarrow 3+5\sqrt{48-10\sqrt{7+4\sqrt{3}}}=3+5(5-\sqrt{3})=28-5\sqrt{3}\)
\(\Rightarrow D=\sqrt{5\sqrt{28-5\sqrt{3}}}\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 9 2019
a/ \(=\left(7+4\sqrt{3}+3\left(7-4\sqrt{3}\right)\right)\left(7+2\sqrt{3}\right)\)
\(=\left(28-8\sqrt{3}\right)\left(7+2\sqrt{3}\right)\)
\(=4\left(7-2\sqrt{3}\right)\left(7+2\sqrt{3}\right)\)
\(=4\left(49-12\right)=...\)
b/ \(=\left(\frac{\sqrt{15}\left(\sqrt{3}-1\right)}{3\left(\sqrt{3}-1\right)}+\frac{2\sqrt{15}}{3}\right).4\sqrt{15}\)
\(=\left(\frac{\sqrt{15}}{3}+\frac{2\sqrt{15}}{3}\right).4\sqrt{15}\)
\(=\sqrt{15}.4\sqrt{15}=4.15=...\)
c/ Bạn coi lại đề
d/ \(\sqrt{23-2\sqrt{112}}+\sqrt{23+2\sqrt{112}}\)
\(=\sqrt{\left(4-\sqrt{7}\right)^2}+\sqrt{\left(4+\sqrt{7}\right)^2}\)
\(=4-\sqrt{7}+4+\sqrt{7}=8\)
20 tháng 6 2021
`a)A=(3-sqrt5)sqrt{3+sqrt5}+(3+sqrt5)sqrt{3-sqrt5}`
`=sqrt{3-sqrt5}sqrt{3+sqrt5}(sqrt{3+sqrt5}+sqrt{3-sqrt5})`
`=sqrt{9-5}(sqrt{3+sqrt5}+sqrt{3-sqrt5})`
`=2(sqrt{3+sqrt5}+sqrt{3-sqrt5})`
`=sqrt2(sqrt{6+2sqrt5}+sqrt{6-2sqrt5})`
`=sqrt2(sqrt{(sqrt5+1)^2}+sqrt{(sqrt5+1)^2})`
`=sqrt2(sqrt5+1+sqrt5-1)`
`=sqrt{2}.2sqrt5`
`=2sqrt{10}`
20 tháng 6 2021
`b)B=(5+sqrt{21})(sqrt{14}-sqrt6)sqrt{5-sqrt{21}}`
`=sqrt{5+sqrt{21}}sqrt{5-sqrt{21}}sqrt{5+sqrt{21}}(sqrt{14}-sqrt6)`
`=sqrt{25-21}sqrt{5+sqrt{21}}(sqrt{14}-sqrt6)`
`=2sqrt{5+sqrt{21}}(sqrt{14}-sqrt6)`
`=2sqrt2sqrt{5+sqrt{21}}(sqrt{7}-sqrt3)`
`=2sqrt{10+2sqrt{21}}(sqrt{7}-sqrt3)`
`=2sqrt{(sqrt3+sqrt7)^2}(sqrt{7}-sqrt3)`
`=2(sqrt3+sqrt7)(sqrt{7}-sqrt3)`
`=2(7-3)`
`=8`
`c)C=sqrt{4+sqrt7}-sqrt{4-sqrt7}`
`=sqrt{(8+2sqrt7)/2}-sqrt{(8-2sqrt7)/2}`
`=sqrt{(sqrt7+1)^2/2}-sqrt{(sqrt7+1)^2/2}`
`=(sqrt7+1)/sqrt2-(sqrt7-1)/2`
`=2/sqrt2=sqrt2`
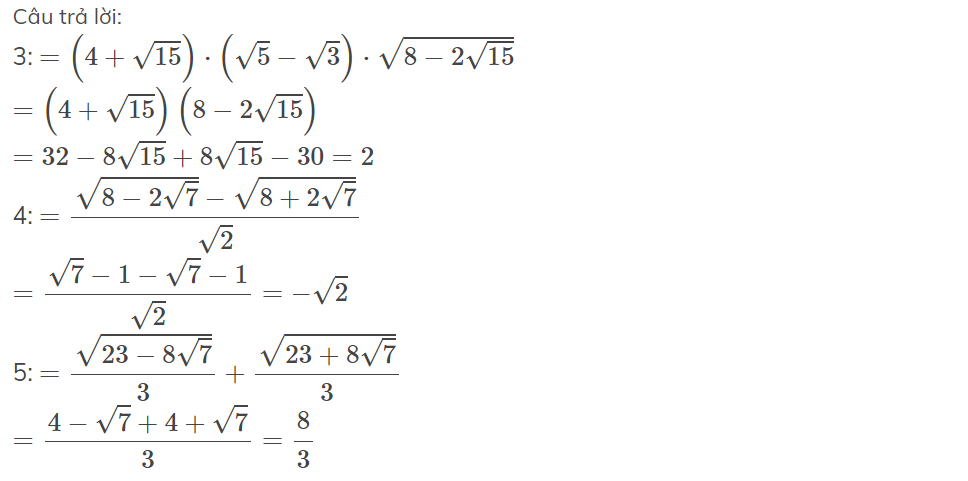
Ta có: \(A=\frac{-\left(\sqrt{7-4\sqrt{3}}+\sqrt{7+4\sqrt{3}}\right)}{\sqrt{7-4\sqrt{3}}-\sqrt{7+4\sqrt{3}}}\)
\(=\frac{-\left(\sqrt{3-2\cdot\sqrt{3}\cdot2+4}+\sqrt{3+2\cdot\sqrt{3}\cdot2+4}\right)}{\sqrt{3-2\cdot\sqrt{3}\cdot2+4}-\sqrt{3+2\cdot\sqrt{3}\cdot2+4}}\)
\(=\frac{-\left(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{\left(\sqrt{3}+2\right)^2}\right)}{\sqrt{\left(\sqrt{3}-2\right)^2}-\sqrt{\left(\sqrt{3}+2\right)^2}}\)
\(=\frac{-\left(\left|\sqrt{3}-2\right|+\left|\sqrt{3}+2\right|\right)}{\left|\sqrt{3}-2\right|-\left|\sqrt{3}+2\right|}\)
\(=\frac{-\left(2-\sqrt{3}+\sqrt{3}+2\right)}{2-\sqrt{3}-\sqrt{3}-2}\)
\(=\frac{-4}{-2\sqrt{3}}=\frac{2\sqrt{3}}{3}\)