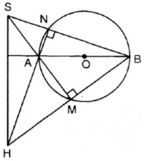
Cho (O), đường kính AB. S là một điểm nằm bên ngoài (O) (S không nằm trên: đường thẳng AB; tiếp tuyến tại A; tiếp tuyến tại B). Cát tuyến SA và SB lần lượt cắt (O) tại 2 điểm M,E. Gọi D là giao điểm của BM và AE.
a) Chứng minh 4 điểm S, M, E, D cùng nằm trên một đường tròn.
b) Chứng minh \(\Delta SME\) đồng dạng với \(\Delta SBA\)
c) Chứng minh SD \(\perp\) AB.
d) Chứng minh các tiếp tuyến tại M và E của đường tròn (O) cắt nhau tại trung điểm của SD




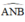 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 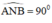 ⇒ AN ⊥ NB
⇒ AN ⊥ NB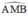 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 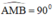 ⇒ AM ⊥ MB
⇒ AM ⊥ MB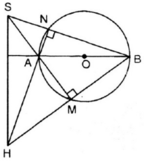
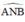 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 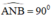 ⇒ AN ⊥ NB
⇒ AN ⊥ NB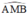 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 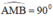 ⇒ AM ⊥ MB
⇒ AM ⊥ MB
giải giúp mik câu d, dới!!!