Tìm tất cả các giá trị của tham số m để bpt -x2+2x-5/ x2-mx+1</ 0 nghiệm đúng với mọi x thuộc R
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trường hợp 1: m=-1
Bất phương trình sẽ là \(0x^2-2\cdot0\cdot x+4>=0\)(luôn đúng)
Trường hợp 2: m<>-1
\(\text{Δ}=\left(2m+2\right)^2-4\cdot4\cdot\left(m+1\right)\)
\(=4m^2+8m+4-16m-16\)
\(=4m^2-8m-12\)
\(=4\left(m^2-2m-3\right)\)
Để bất phương trình có nghiệm đúng với mọi x thực thì \(\left\{{}\begin{matrix}\left(m-3\right)\left(m+1\right)< 0\\\left(m+1\right)>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-1< m< 3\\m>=-1\end{matrix}\right.\Leftrightarrow-1< m< 3\)
Vậy: -1<=m<3

Đặt \(x^2+4x+3=t\left(t\ge-1\right)\)
\(\left(x^2+4x+3\right)\left(x^2+4x+6\right)\ge m,\forall x\in R\)
\(\Leftrightarrow\left(x^2+4x+3\right)^2+3\left(x^2+4x+3\right)\ge m,\forall x\in R\)
\(\Leftrightarrow m\le f\left(t\right)=t^2+3t,\forall x\in R\)
Yêu cầu bài toán thỏa mãn khi:
\(m\le minf\left(t\right)=-2\)

Lời giải:
$f(x)=m^2(x^4-1)+m(x^2-1)-6(x-1)=(x-1)[m^2(x+1)(x^2+1)+m(x+1)-6]$
Để $f(x)\geq 0$ với mọi $x\in\mathbb{R}$ thì:
$m^2(x+1)(x^2+1)+m(x+1)-6=Q(x)(x-1)^k$ với $k$ là số lẻ
$\Rightarrow h(x)=m^2(x+1)(x^2+1)+m(x+1)-6\vdots x-1$
$\Rightarrow h(1)=0$
$\Leftrightarrow 4m^2+2m-6=0$
$\Leftrightarrow 2m^2+m-3=0$
$\Leftrightarrow (m-1)(2m+3)=0\Rightarrow m=1$ hoặc $m=\frac{-3}{2}$
Thay các giá trị trên vào $f(x)$ ban đầu thì $m\in \left\{1; \frac{-3}{2}\right\}$
Tổng các giá trị của các phần tử thuộc $S$: $1+\frac{-3}{2}=\frac{-1}{2}$

Phương trình đã cho nghiệm đúng với hay phương trình có vô số nghiệm khi
m 2 − 3 m + 2 = 0 − ( m 2 + 4 m + 5 ) = 0 ⇔ m = 1 m = 2 m ∈ ∅ ⇔ m ∈ ∅
Đáp án cần chọn là: D

Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 

Đáp án D
Để bất phương trình m ≤ f x = x 2 + 3 x + 3 x + 1 ; ∀ x ∈ 0 ; 1 ⇔ m ≤ min 0 ; 1 f x
Xét hàm số f x = x 2 + 3 x + 3 x + 1 trên 0 ; 1 ⇒ min 0 ; 1 f x = 3 . Vậy m ≤ 3

Bài 2:
Để phương trình có hai nghiệm trái dấu thì (m-2)(m+2)<0
hay -2<m<2
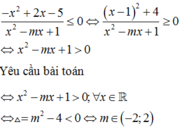
Do \(-x^2+2x-5=-\left(x-1\right)^2-4< 0;\forall x\) nên BPT tương đương:
\(x^2-mx+1>0\) ; \(\forall x\in R\)
\(\Leftrightarrow\Delta=m^2-4< 0\Rightarrow-2< m< 2\)
Lưu ý là</: dấu nhỏ hơn hoặc bằng