Cách tính 40÷60 ra phân số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\frac{1}{5}+\frac{1}{7}+\frac{1}{3}+\frac{100}{125}+\frac{66}{77}+\frac{40}{60}\)
\(=\frac{1}{5}+\frac{1}{7}+\frac{1}{3}+\frac{4}{5}+\frac{6}{7}+\frac{2}{3}\)
\(=\left(\frac{1}{5}+\frac{4}{5}\right)+\left(\frac{1}{7}+\frac{6}{7}\right)+\left(\frac{1}{3}+\frac{2}{3}\right)\)
\(=1+1+1\)
\(=3\)

A : Dãy số cách đều 4 đơn vị
B: Dãy số cách đều 5 đơn vị
C: Dãy số cách đều 10 dơn vị
D : dãy số cách đều 5 đơn vị

Vì Oz là phân giác của góc xOy
\(\Rightarrow\) xOz = zOy = \(\frac{1}{2}\) xOy = \(\frac{1}{2}.60^o=30^o\)
Trên cùng một nửa mặt phẳng có bờ chứa tia Ox
Ta có: xOy < xOn (60o<80o)
\(\Rightarrow\) Oy nằm giữa Ox và On
Ta có: xOy + yOn = xOn
60o + yOn = 80o
yOn = 80o - 60o = 20o
Vì Oy nằm giữa Ox và On
Vì Oz nằm giữa Ox và Oy
\(\Rightarrow\) Oy nằm giữa Oz và On
Ta có: zOy + yOn = zOn
30o + 20o = zOn
zOn = 50o

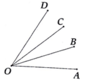
a) Ta có A O B ^ < A O C ^ nên tia OB nằm giữa hai tia OA và OC. Theo tính chất cộng góc, suy ra 20°, nên A O B ^ = B O C ^ . Vậy OB là tia phân giác của góc AOC.
b) Tương tự ý a), tính được
C O D ^ = 20° và B O D ^ = 40°.
c) Ta có B O C ^ = C O D ^ = B O D ^ 2 (cùng bằng 20°). Do đó, tia OC là tia phân giác của góc BOD.