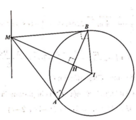
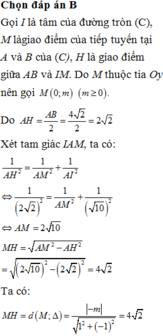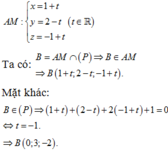trong mặtphẳng Oxy cho đường thẳng \(\Delta\) x-y=0. Đường tròn (C) có bán kính R=\(\sqrt{10}\) cắt \(\Delta\)tại 2 điểm A,B sao cho AB=4\(\sqrt{2}\). tiếp tuyến của (C) tại A, B cắt nhau tại một điểm thuộc tia Oy. Viết phương trình đường tròn (C)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 12 2023
a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
nên MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
b: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại K
Xét ΔOAM vuông tại A có AK là đường cao
nên \(OK\cdot OM=OA^2=R^2\)
Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{MAO}=90^0\)
\(\widehat{KAI}+\widehat{OIA}=90^0\)(ΔAKI vuông tại K)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{KAI}\)
=>AI là phân giác của góc MAB
Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MO là phân giác của góc AMB
=>MK là phân giác của góc AMB
Xét ΔMAB có
MK,AI là các đường phân giác
MK cắt AI tại I
Do đó: I là tâm đường tròn nội tiếp ΔMAB
13 tháng 6 2023
2: góc OME+góc OAE=180 độ
=>OMEA nội tiếp
=>góc AOE=góc AME=góc OMB