Cho đg tròn (C) có tâm I thuộc trục Ox và đi qua 2 điểm M(1;-2), N(3;-1). Viết pt đg tròn (C)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

18 tháng 3 2021
a) Xét (O) có
\(\widehat{CDA}\) là góc nội tiếp chắn \(\stackrel\frown{CA}\)
\(\widehat{ABC}\) là góc nội tiếp chắn \(\stackrel\frown{CA}\)
Do đó: \(\widehat{CDA}=\widehat{ABC}\)(Hệ quả góc nội tiếp)
hay \(\widehat{MDA}=\widehat{MBC}\)
Xét ΔMAD và ΔMCB có
\(\widehat{MDA}=\widehat{MBC}\)(cmt)
\(\widehat{AMD}\) chung
Do đó: ΔMAD\(\sim\)ΔMCB(g-g)
Suy ra: \(\dfrac{MA}{MC}=\dfrac{MD}{MB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(MA\cdot MB=MC\cdot MD\)(đpcm)

CM
14 tháng 2 2018
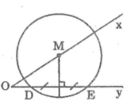
* Cách dựng:
- Dựng đường trung trực của DE cắt Ax tại M
- Dựng đường tròn tâm M bán kính MD
* Chứng minh:
Theo cách dựng ta có: M ∈ Ox
MD = ME (tính chất đường trung trực)
Suy ra: E ∈ (M; MD).



Gọi A là trung điểm \(MN\Rightarrow A\left(2;-\frac{3}{2}\right)\)
\(\overrightarrow{MN}=\left(2;1\right)\)
Trung trực d của MN đi qua A và vuông góc MN có pt:
\(2\left(x-2\right)+1\left(y+\frac{3}{2}\right)=0\Leftrightarrow2x+y-\frac{5}{2}=0\)
I là giao của d và Ox nên tọa độ thỏa mãn: \(\left\{{}\begin{matrix}y=0\\2x+y-\frac{5}{2}=0\end{matrix}\right.\)
\(\Rightarrow I\left(\frac{5}{4};0\right)\) \(\Rightarrow\overrightarrow{AI}=\left(\frac{1}{4};2\right)\Rightarrow R=\sqrt{\left(\frac{1}{4}\right)^2+2^2}=\frac{\sqrt{65}}{4}\)
Phương trình: \(\left(x-\frac{5}{4}\right)^2+y^2=\frac{65}{16}\)