Cho các đa thức :
A(x) = \(x^3\)- 2x2 + x - m + 2
B(x) = x + 3
Tìm m để đa thức A(x) chia cho đa thức B(x) có số dư bằng 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\Leftrightarrow4x^3-2x^2+a=\left(2x-3\right).a\left(x\right)\)
Thay \(x=\dfrac{3}{2}\Leftrightarrow4.\dfrac{27}{8}-2.\dfrac{9}{4}+a=0\)
\(\Leftrightarrow\dfrac{27}{2}-\dfrac{9}{2}+a=0\\ \Leftrightarrow a=-9\)
\(b,\Leftrightarrow3x^3+2x^2+x+a=\left(x+1\right).b\left(x\right)+2\)
Thay \(x=-1\Leftrightarrow-3+2-1+a=2\Leftrightarrow a=4\)

Ta có A(x) chia cho B(x) có số dư là 5
=> A(x) = C(x). (x+3) + 5
=> A(-3) = 5 => (-3)3 + 2.(-3)2 + (-3) + 2 - m=5
=>(-10) - m =0 => m = -10

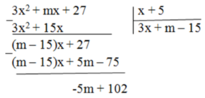
A(x) chia cho B(x) có số dư bằng 2 nên 102 – 5m = 2 ⇒ -5m = 100
⇒ m = 20

a: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)

b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
