cho hai đường thẳng \(d_1\) :mx+y=m+1 và \(d_2\) : x+my=2 song song với nhau khi và chỉ khi ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
+ Để 2 đường thẳng đã cho song song với nhau thì:
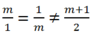
Mà m 1 = 1 m nếu m2= 1 hay m = ± 1
+ Khi m= 1 ta có: 1 1 = 1 1 = 2 2 khi đó 2 đường thẳng đã cho trùng nhau ( loại ).
+ Khi m= -1 ta có: - 1 1 = 1 - 1 ≠ 0 2 khi đó 2 đường thẳng đã cho song song với nhau.

Hệ số góc của đường thẳng \({d_1}:y = 0,2x\) là \(a = 0,2\);
Hệ số góc của đường thẳng \({d_2}:y = - 2x + 4\) là \(a = - 2\);
Hệ số góc của đường thẳng \({d_3}:y = 0,2x - 0,8\) là \(a = 0,2\);
Hệ số góc của đường thẳng \({d_4}:y = - 2x - 5\) là \(a = - 2\);
Hệ số góc của đường thẳng \({d_5}:y = \sqrt 3 x + 3\) là \(a = \sqrt 3 \);
Hệ số góc của đường thẳng \({d_6}:y = \sqrt 3 x - \sqrt 5 \) là \(a = \sqrt 3 \);
- Các cặp đường thẳng song song là:
\({d_1}:y = 0,2x\) và \({d_3}:y = 0,2x - 0,8\) vì đều có hệ số góc \(a = 0,2\) và chúng phân biệt vì cắt \(Oy\) tại hai điểm khác nhau.
\({d_2}:y = - 2x + 4\) và \({d_4}:y = - 2x - 5\) vì đều có hệ số góc \(a = - 2\)và chúng phân biệt vì cắt \(Oy\) tại hai điểm khác nhau.
\({d_5}:y = \sqrt 3 x + 3\) và \({d_6}:y = \sqrt 3 x - \sqrt 5 \) vì đều có hệ số góc \(a = \sqrt 3 \) và chúng phân biệt vì cắt \(Oy\) tại hai điểm khác nhau.
- Ba cặp đường thẳng cắt nhau là:
\({d_1}:y = 0,2x\) và \({d_2}:y = - 2x + 4\) vì có hệ số góc khác nhau \(\left( {0,2 \ne - 2} \right)\).
\({d_3}:y = 0,2x - 0,8\) và \({d_4}:y = - 2x - 5\)vì có hệ số góc khác nhau \(\left( {0,2 \ne - 2} \right)\).
\({d_5}:y = \sqrt 3 x + 3\) và \({d_4}:y = - 2x - 5\) vì có hệ số góc khác nhau \(\left( {\sqrt 3 \ne - 2} \right)\).
Ba cặp đường thẳng cắt nhau: d1 và d2, d2 và d3, d4 và d5
Các cặp đường thẳng song song: d1 và d3, d2 và d4, d5 và d6

a/ Để \(d_1//d_2\Leftrightarrow\left\{{}\begin{matrix}m=3\\2\ne-1\end{matrix}\right.\) \(\Leftrightarrow m=3\)
b/ Để d1 cắt d2 \(\Leftrightarrow m\ne3\)
c/ Để d1 vuông góc d2 \(\Leftrightarrow m.3=-1\Leftrightarrow m=-\frac{1}{3}\)
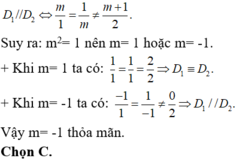
Lời giải:
Hai đường thẳng trên song song với nhau khi mà\(\left\{\begin{matrix} m\neq 0\\ \frac{m}{1}=\frac{1}{m}\\ m+1\neq 2\end{matrix}\right.\Leftrightarrow m=-1\)