Cho điểm M(9;4). Viết phương trình đường thẳng qua M, cắt 2 tia Ox và Oy tại A và B sao cho diện tích tam giác OAB nhỏ nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


N đối xứng M qua P \(\Leftrightarrow\) P là trung điểm MN
\(\Rightarrow\left\{{}\begin{matrix}x_N=2x_P-x_M=18\\y_N=2y_P-y_M=-10\end{matrix}\right.\) \(\Rightarrow N\left(18;-10\right)\)

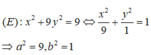
Ta có: c2 = a2 - b2 = 9 - 1 = 8 ⇒ c = 2√2
⇒ F1(-2√2;0), F2(2√2;0)
Tìm trên (E) điểm M sao cho MF1 = 2MF2
Giả sử M(x;y) là điểm thỏa mãn yêu cầu của đề bài
Vì M thuộc (E) nên:
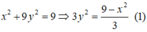
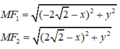
Theo đề bài ta có:
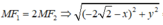
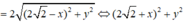
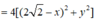
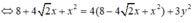
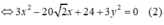
Thay (1) vào (2) ta được:
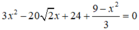
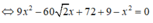
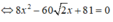
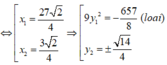
Vậy có hai điểm thỏa mãn đề bài là:
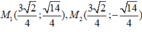

Do điểm M’ đối xứng với điểm M qua điểm P nên P là trung điểm MM’.
Suy ra:
x P = x M + x M ' 2 y P = y M + y M ' 2 ⇔ x M ' = 2 x P − x M = 2.9 − 0 = 18 y M ' = 2 y P − y M = 2. ( − 3 ) − 4 = − 10 ⇒ M ' ( 18 ; − 10 )
Đáp án B

Lời giải:
Vì $K\in$ đths nên $y_K=-2x_K+9$
$\Leftrightarrow 3+m^2=-2m^2+9$
$\Leftrightarrow 3m^2=6$
$\Leftrightarrow m^2=2$
Khi đó $K(m^2, 3+m^2)=K(2, 5)$

Đáp án là B.
Gọi M 0 ; y ; 0 ∈ O y .
Ta có: A M → = − 1 ; y − 1 ; − 2 ;
B M → = 1 ; y − 3 ; 9 ; A M → . B M → = − 1 + y − 1 y − 3 − 18
Tam giác ABM vuông tại A
⇔ y 2 − 4 y − 16 = 0 ⇔ y = 2 + 2 5 y = 2 − 2 5
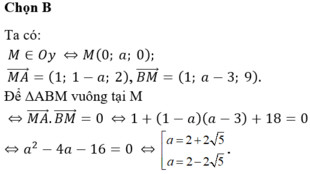
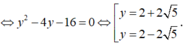
Gọi đường thẳng d qua M cắt hai tia Ox, Oy có dạng \(y=-kx+b\) (\(k\ne0\))
d qua M nên: \(4=-9k+b\Rightarrow b=9k+4\)
\(\Rightarrow y=-kx+9k+4\)
Tọa độ A: \(A\left(\frac{9k+4}{k};0\right)\) ; tọa độ B: \(B\left(0;9k+4\right)\)
Để A; B nằm trên 2 tia Ox; Oy \(\Leftrightarrow\left\{{}\begin{matrix}\frac{9k+4}{k}>0\\9k+4>0\end{matrix}\right.\) \(\Rightarrow k>0\)
Khi đó: \(S_{OAB}=\frac{1}{2}\left(\frac{9k+4}{k}\right).\left(9k+4\right)=\frac{1}{2}\left(\frac{81k^2+16+72k}{k}\right)\)
\(S=\frac{1}{2}\left(81k+\frac{16}{k}\right)+36\ge\frac{1}{2}.2\sqrt{\frac{81k.16}{k}}+32=68\)
Dấu "=" xảy ra khi \(81k=\frac{16}{k}\Leftrightarrow k^2=\frac{16}{81}\Rightarrow k=\frac{4}{9}\)
Phương trình d: \(y=-\frac{4}{9}x+8\Leftrightarrow4x+9y-72=0\)