sin6o .cos 12o .cos24o.cos 48o = ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HV
29 tháng 8 2021
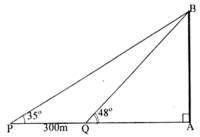
a,35+55=90 nên sin 35=cos 55
b,12+78=90 nên tan 12 =cot 78
tik mik nha
O
25 tháng 3 2018
gọi a là số gam CuSO4 thêm vào (1)
Mdd=vddXD = 400 X 1.1 = 440(g)
>>>mCt=440X10/100=44(g)
>>>mH20=440-44=396(g)
ta có :
C%=(a + 44) X100%/ (440 + a)=28.8%
>>>>4400 +100a = 12672 + 28.8a
>>>>8272 =71.2a
>>>>a=116.18 (g)
trong 250g CuSO4.5H20 _________________90g H20
_____60g_____________________________21.6g H20
>>>mCuSO4 = 60- 21.6 = 38.4 (g)
>>>mct=116.18 + 44 -38.4 = 121.18(g)
>>>mH20 =396 - 21.6 =374.4(g)
áp dụng CT ta có
S=121.18X100/374.4=32.5 (g)
29 tháng 10 2021
Ta có \(\sin B=\sin48^0=\dfrac{AC}{BC}\approx0,74\Leftrightarrow BC\approx\dfrac{12}{0,74}\approx16,22\left(cm\right)\)
Áp dụng PTG: \(AB=\sqrt{BC^2-AC^2}\approx10,91\left(cm\right)\)
\(\widehat{C}=90^0-\widehat{B}=42^0\)
15 tháng 10 2017
Gọi CTHH của hợp chất A là X2S3O12
Ta có MA =MX.2+MS.3+MO.12
=MX.2+32.3+16.12
=MX.2+288=342 đvC
=>MX=27 đvC
Vậy X là nhôm(Al) và CTHH của hợp chất A là Mg2S3O12
10 tháng 9 2017
Bài giải
Số gạo dự trữ đó đủ cho một người ăn trong số ngày là:
120 x 20 = 2400 ( ngày )
Số gạo dự trữ đó đủ cho 150 người ăn trong số ngày là :
2400 : 150 = 16 ( ngày )
Đáp số : 16 ngày
10 tháng 9 2017
Một người ăn trong số ngày là:
120 x 20 = 2400 ( ngày )
150 người ăn trong số ngày là:
2400 : 150 = 16 ( ngày )
Đáp số: 16 ngày
S
11 tháng 11 2018
Gọi 5 số tự nhiên liên tiếp là: a;a+1;a+2;a+3;a+4
Trong 5 số tự nhiên liên tiếp ít nhất có 2 số chẵn và 1 số chia hết cho 2 và 1 số chia hết cho 4
=> a(a+1)(a+2)(a+3)(a+4) chia hết cho: 2.4=8
=>a(a+1)(a+2)(a+3)(a+4) mà trong 5 số tự nhiên liên tiếp có 1 số chia hết cho 3
=> a(a+1)(a+2)(a+3)(a+4) chia hết cho 3.8=24 vì 3 và 8 là 2 số nguyên tố cùng nhau
trong 5 số tự nhiên liên tiếp sẽ có 1 số chia hết cho 5
=> a(a+1)(a+2)(a+3)(a+4) chia hết cho 5.24=120 vì 24 và 5 là 2 số nguyên tố cùng nhau
(đpcm)
Đặt \(A=sin6.cos12.cos24.cos48\)
\(\Rightarrow A.cos6=sin6.cos6.cos12.cos24.cos48\)
\(A.cos6=\frac{1}{2}sin12.cos12.cos24.cos48\)
\(A.cos6=\frac{1}{4}sin24.cos24.cos48=\frac{1}{8}sin48.cos48\)
\(A.cos6=\frac{1}{16}sin96=\frac{1}{16}cos6\)
\(\Rightarrow A=\frac{1}{16}\)