tìm các giá trị nguyên của x thỏa mãn bất phương trình sau: (x+1).(x-1)<0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


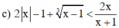
BPT xác định khi x + 1 ≠ 0 ⇔ x ≠ –1.
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–1}

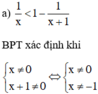
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{0; –1}

Điều kiện 1 3 ≤ x ≤ 10
Bất phương trình đã cho tương đương với:
log 2 3 x + 1 + 6 - 1 ≥ log 2 7 - 10 - x ⇔ 3 x + 1 + 6 2 ≥ 7 - 10 - x ⇔ 3 x + 1 + 2 10 - x ≥ 8 ⇔ 3 x + 1 + 4 3 x + 1 10 - x + 4 10 - x ≥ 64 ⇔ 4 3 x + 1 10 - x ≥ x + 23 ⇔ 16 3 x + 1 10 - x ≥ x + 23 2 ⇔ 49 x 2 - 418 x + 369 ≤ 0 ⇔ 1 ≤ x ≤ 369 49 ≈ 7 , 5
Mà x ∈ ℤ nên x ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7
Vậy có 7 giá trị nguyên của x
Đáp án D

Chọn D.
Với m = 1 hệ bất phương trình trở thành:
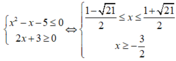
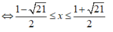
Vậy tập nghiệm hệ bất phương trình là
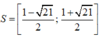

Ta có Từ (1)<=>7x-4x<8+4
<=>3x<12
<=>x<4 (3)
Từ (2) <=> 10x-12x >-8-15
<=>-2x > -23
<=>x > -11,5(4)
Từ (3), (4) suy ra -11.5<x<4 mà x >0 nên 0<x<4

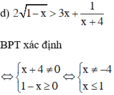
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = (–∞; 1] \ {–4}.
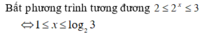
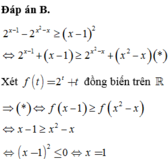
\(\left(x+1\right)\left(x-1\right)< 0\)
\(\Leftrightarrow x^2-1< 0\)
\(\Leftrightarrow x^2< 1\)
\(\Leftrightarrow\hept{\begin{cases}x< 1\\x>-1\end{cases}}\)
Vậy giá trị thỏa mãn của x là 0