Trong mặt phẳng chứa hệ trục tọa độ Oxy, cho hình bình hành ABCD có đỉnh A thuộc đường thẳng d: x= 1-t y=3+ 2t , B(0,1); C(5;3). Tính độ dài đoạn thẳng OA biết rằng đường thẳng AD đi qua điểm K(2,4)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 4 2016
Ta có \(\widehat{AHC}=\widehat{AEC}=90^0\) nên 4 điểm A, H, C, E cùng thuộc đường tròn đường kính AC.
Gọi I là giao điểm của AC và BD
Ta có \(\widehat{HIE}=2\widehat{HAE}=2\left(180^0-\widehat{BCD}\right)\)
Các tứ giác AKED, AKHB nội tiếp nên \(\widehat{EKD}=\widehat{EAD}\) và \(\widehat{BKH}=\widehat{BAH}\)
Do đó \(\widehat{HKE}=180^0-\widehat{AKD}-\overrightarrow{BKH}=180^0-\overrightarrow{EAD}-\overrightarrow{BAH}=2\overrightarrow{HAE}=2\left(180^0-\overrightarrow{BCD}\right)=\overrightarrow{HIE}\)
Vậy tứ giác HKIE nội tiếp. Do đó I thuộc đường tròn (C) ngoại tiếp tam giác HKE
- Gọi \(C\left(c;c-3\right)\in d\left(c>0\right)\Rightarrow I\left(\frac{c-2}{2};\frac{c-4}{2}\right)\)
Do I thuộc (C) nên có phương trình :
\(c^2-c-2=0\Leftrightarrow c=2\) V c=-1 (loại c=-1) Suy ra \(C\left(2;-1\right);I\left(0;-1\right)\)
- Điểm E, H nằm trên đường tròn đường kính AC và đường tròn (C) nên tọa độ thỏa mãn hệ phương trình :
\(\begin{cases}x^2+y^2+x+4y+3=0\\x^2+\left(y+1\right)^2=4\end{cases}\) \(\Leftrightarrow\begin{cases}x=0;y=-3\\x=-\frac{8}{5};y=-\frac{11}{2}\end{cases}\)
- Vì H có hoành độ âm nên \(H\left(-\frac{8}{5};-\frac{11}{5}\right);E\left(0;-3\right)\) Suy ra \(AB:x-y+1=0;BC:x-3y-5=0\)
Tọa độ B thỏa mãn \(\begin{cases}x-y+1=0\\x-3y-5=0\end{cases}\) \(\Leftrightarrow B\left(-4;-3\right)\Rightarrow\overrightarrow{BA}=\left(2;2\right);\overrightarrow{BC}=\left(6;2\right)\Rightarrow\overrightarrow{BA}.\overrightarrow{BC}=16>0\)
Vì \(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow D\left(4;1\right)\)
Vậy \(B\left(-4;-3\right);C\left(2;-1\right);D\left(4;1\right)\)
MK
20 tháng 12 2021
1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)
16 tháng 5 2021
1. \(\overrightarrow{AH}\left(\frac{96}{37};\frac{16}{37}\right)\). AB và CD cùng vuông góc với AH => AB,CD có VTPT cùng phương với vt AH
Đường thẳng AB: đi qua A(1;-2), VTPT (6;1) => \(AB:6\left(x-1\right)+\left(y+2\right)=0\Leftrightarrow6x+y-4=0\)
Đường thẳng CD: đi qua H(133/37;-58/37), VTPT (6;1)
=> \(CD:6\left(x-\frac{133}{37}\right)+\left(y+\frac{58}{37}\right)=0\Leftrightarrow6x+y-20=0\)
2. Xét hệ \(\hept{\begin{cases}2x+y=4\\6x+y=4\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=4\end{cases}\Rightarrow}B\left(0;4\right)}\)
\(\hept{\begin{cases}2x+y=4\\6x+y=20\end{cases}\Leftrightarrow\hept{\begin{cases}x=4\\y=-4\end{cases}\Rightarrow}D\left(4;-4\right)}\)
BD và AC có trung điểm là \(I\left(2;0\right)\), suy ra \(C\left(3;2\right)\).
3. Ta có: \(MA^2+MC^2=2MI^2+\frac{AC^2}{2};MB^2+MD^2=2MI^2+\frac{BD^2}{2}\)
\(\Rightarrow MA^2+MB^2+MC^2+MD^2=4MI^2+\frac{AC^2+BD^2}{2}\ge\frac{AC^2+BD^2}{2}\)(không đổi)
Vậy biểu thức đạt Min khi M trùng với I(3;2).
19 tháng 5 2021
1. →AH(9637 ;1637 ). AB và CD cùng vuông góc với AH => AB,CD có VTPT cùng phương với vt AH
Đường thẳng AB: đi qua A(1;-2), VTPT (6;1) => AB:6(x−1)+(y+2)=0⇔6x+y−4=0
Đường thẳng CD: đi qua H(133/37;-58/37), VTPT (6;1)
=> CD:6(x−13337 )+(y+5837 )=0⇔6x+y−20=0
2. Xét hệ {
| 2x+y=4 |
| 6x+y=4 |
⇔{
| x=0 |
| y=4 |
⇒B(0;4)
{
| 2x+y=4 |
| 6x+y=20 |
⇔{
| x=4 |
| y=−4 |
⇒D(4;−4)
BD và AC có trung điểm là I(2;0), suy ra C(3;2).
3. Ta có: MA2+MC2=2MI2+AC22 ;MB2+MD2=2MI2+BD22
⇒MA2+MB2+MC2+MD2=4MI2+AC2+BD22 ≥AC2+BD22 (không đổi)
Vậy biểu thức đạt Min khi M trùng với I(3;2).
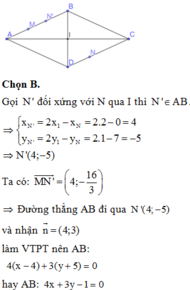
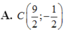
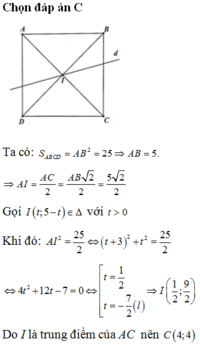
Ta có: \(\overrightarrow{u_d}=\left(-1;2\right)=>\overrightarrow{n_d}\left(2;1\right)\)
(d): 2x + y -5 =0
Phương trình AD qua K và // BC: 5x + 2y -18 = 0
=> Tọa độ điểm A là nghiệm của hệ: \(\left\{{}\begin{matrix}2x+y-5=0\\5x+2y-18=0\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}x=8\\y=-11\end{matrix}\right.\) => A(8; -11)
=> OA = \(\sqrt{\left(0-8\right)^2+\left(0+11\right)^2}\) = \(\sqrt{185}\)