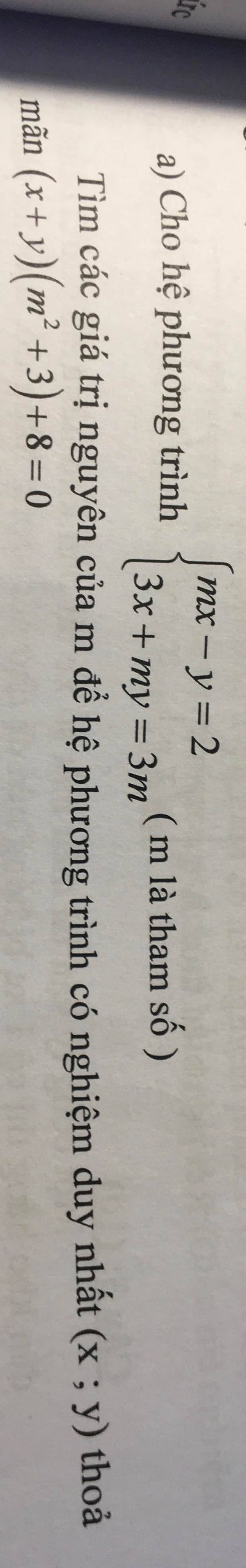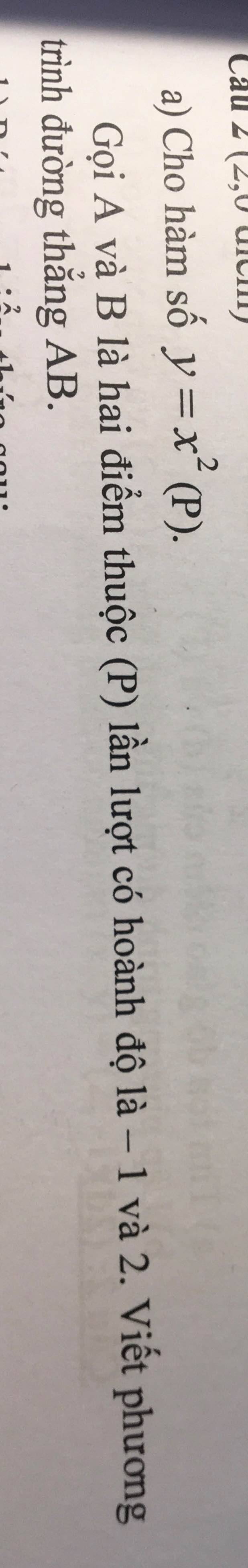Làm hộ mình với ạ, đề dưới phần bình luận
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NK
Nguyễn Khánh Huyền
24 tháng 5 2020
Đúng(0)
Những câu hỏi liên quan
HL
3
8 tháng 12 2023
Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{3}< >-\dfrac{1}{m}\)
=>\(m^2\ne-3\)(luôn đúng)
Ta có: \(\left\{{}\begin{matrix}mx-y=2\\3x+my=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m\left(mx-2\right)=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m^2x-2m=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+3\right)=5m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=m\cdot\dfrac{5m}{m^2+3}-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=\dfrac{5m^2-2m^2-6}{m^2+3}=\dfrac{3m^2-6}{m^2+3}\end{matrix}\right.\)
\(\left(x+y\right)\cdot\left(m^2+3\right)+8=0\)
=>\(\dfrac{5m+3m^2-6}{m^2+3}\cdot\left(m^2+3\right)+8=0\)
=>\(3m^2+5m-6+8=0\)
=>\(3m^2+5m+2=0\)
=>(m+1)(3m+2)=0
=>\(\left[{}\begin{matrix}m=-1\\m=-\dfrac{2}{3}\end{matrix}\right.\)
NN
29 tháng 12 2022
a, Diện tích khu vườn hình thang là:
\(\left(60+80\right)\times50:2=3500m^2\)
b, Diện tích bồn đất trồng hoa là:
\(18\times25=450m^2\)
c,Ta có: \(450=200.2+50\)
Vậy cần ít nhất 3 túi giống rau để gieo hết phần đất trồng rau.
NK
1
M
1
PT
2
9 tháng 11 2023
\(M=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{100}}\)
=>\(2M=1+\dfrac{1}{2}+...+\dfrac{1}{2^{99}}\)
=>\(2M-M=1+\dfrac{1}{2}+...+\dfrac{1}{2^{99}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{100}}\)
=>\(M=1-\dfrac{1}{2^{100}}< 1\)
HT
3
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 5 2020
Với mọi x;y;z ta luôn có:
\(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)
\(\Leftrightarrow2x^2+2y^2+2z^2-2xy-2yz-2zx\ge0\)
\(\Leftrightarrow x^2+y^2+z^2\ge xy+yz+zx\)
\(\Leftrightarrow x^2+y^2+z^2+2\left(xy+yz+zx\right)\ge3\left(xy+yz+zx\right)\)
\(\Leftrightarrow\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\)
\(\Rightarrow xy+yz+zx\le\frac{\left(x+y+z\right)^2}{3}=\frac{3^2}{3}=3\)
\(B_{max}=3\) khi \(x=y=z=1\)
