Trong Oxy, cho ΔABC vuông cân tại A, có trọng tâm G (\(\frac{2}{3}\);0). Biết M(1;-1) là trung điểm của BC. Tìm tọa độ các đỉnh của ΔABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
23 tháng 4 2018
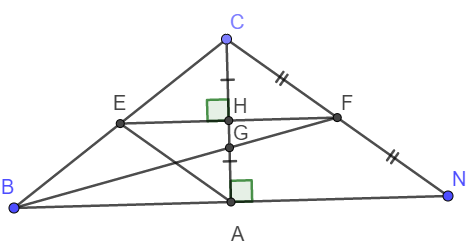
a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 = AC2 + AB2
252 = 152 + AB2 \(\Rightarrow ab=20\left(cm\right)\)
Xét tam giác ABC có:
AC < AB < BC nên \(\widehat{CBA}< \widehat{BCA}< \widehat{BAC}.\)
b) Xét tam giác vuông EHA và tam giác vuông EHC có:
Cạnh EH chung
HC = HA
\(\Rightarrow\Delta EHC=\Delta EHA\) (Hai cạnh góc vuông)
Do \(\Delta EHC=\Delta EHA\Rightarrow\widehat{ECA}=\widehat{EAC}\)
\(\Rightarrow\widehat{EBA}=\widehat{EAB}\) (Cùng phụ với hai góc bên trên)
Vậy nên tam giác EAB cân tại E.
c) Tam giác CBN cân tại C có CA là đường cao nên CA đồng thời là trung tuyến.
Xét tam giác CBN có CA và BF là các đường trung tuyến mà CA giao BF tại G nên G là trọng tâm tam giác.
Theo tính chất trọng tâm ta có:
\(\frac{AG}{AC}=\frac{1}{3}\Rightarrow AG=\frac{1}{5}.15=5\left(cm\right)\)
d) Xét tam giác CBN cân tại C có CA là đường cao nên đồng thời là phân giác.
Gọi giao điểm của EH với CN là F'. Khi đó ta có \(\Delta ECH=\Delta F'CH\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow CE=CF'\)
Lại có \(CE=\frac{1}{2}BC=\frac{1}{2}CN\Rightarrow CF'=\frac{1}{2}CN\)
Suy ra F' là trung điểm CN hay F' trùng F.
Vậy nên E, H, FA thẳng hàng.
T
17 tháng 8 2018
Bài giải :
a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 = AC2 + AB2
252 = 152 + AB2 ⇒ab=20(cm)
Xét tam giác ABC có:
AC < AB < BC nên ^CBA<^BCA<^BAC.
b) Xét tam giác vuông EHA và tam giác vuông EHC có:
Cạnh EH chung
HC = HA
⇒ΔEHC=ΔEHA (Hai cạnh góc vuông)
Do ΔEHC=ΔEHA⇒^ECA=^EAC
⇒^EBA=^EAB (Cùng phụ với hai góc bên trên)
Vậy nên tam giác EAB cân tại E.
c) Tam giác CBN cân tại C có CA là đường cao nên CA đồng thời là trung tuyến.
Xét tam giác CBN có CA và BF là các đường trung tuyến mà CA giao BF tại G nên G là trọng tâm tam giác.
Theo tính chất trọng tâm ta có:
AGAC =13 ⇒AG=15 .15=5(cm)
d) Xét tam giác CBN cân tại C có CA là đường cao nên đồng thời là phân giác.
Gọi giao điểm của EH với CN là F'. Khi đó ta có ΔECH=ΔF'CH (Cạnh góc vuông và góc nhọn kề)
⇒CE=CF'
Lại có CE=12 BC=12 CN⇒CF'=12 CN
Suy ra F' là trung điểm CN hay F' trùng F.
Vậy nên E, H, FA thẳng hàng.
CM
16 tháng 6 2017
Đáp án B
=> Đường thẳng AB có pt là: x- y – 5= 0.
Gọi G(a;3a- 8) suy ra C( 3a- 5; 9a -19).
Ta có:
Vậy C( 1 ; -1) và C( -2 ; 10)
