Tìm giá trị nhỏ nhất m của hàm số f(x) = \(\frac{2x^2+4}{x}\)với x>0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
1
14 tháng 1 2020
f(x) = x3 +3/x = x3 + 1/x +1/x +1/x
cô si 4 số làm mất x là xong
14 tháng 3 2021
Ta có \(f\left(x\right)-6=\dfrac{2x^3+4-6x}{x}=\dfrac{2\left(x-1\right)^2\left(x+2\right)}{x}\ge0\) nên \(f\left(x\right)\ge6\).
Đẳng thức xảy ra khi và chỉ khi x = 1.
14 tháng 3 2021
Cách khác thì dùng AM - GM:
\(f\left(x\right)=2x^2+\dfrac{4}{x}=2x^2+\dfrac{2}{x}+\dfrac{2}{x}\ge3\sqrt[3]{2x^2.\dfrac{2}{x}.\dfrac{2}{x}}=6\).
Xảy ra đẳng thức khi x = 1.
14 tháng 1 2020
tách x2+32 = (x2-4) +32
=) f(x) = (x+2)/4 + 9/(x-2) = [(x-2)/4 +9/(x-2)] + 1
cô si 2 số trong ngoặc vuông làm mất (X-2) là xong
NN
0
CM
14 tháng 11 2017
+ Đạo hàm f'(x) = 2 - m x 2 ( x + 1 ) x ( x + 1 )
f'(x) = 0 ⇒ x = 2 m ↔ x = m 2 4 ∈ [ 0 ; 4 ] , ∀ m > 1
+ Lập bảng biến thiên, ta kết luận được
m a x [ 0 ; 4 ] f ( x ) = f ( 4 m 2 ) = m 2 + 4
+ Vậy ta cần có m 2 + 4 < 3
↔ m < 5 → m > 1 m ∈ ( 1 ; 5 )
Chọn C.
CM
18 tháng 4 2019
Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
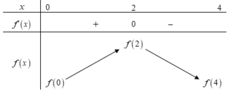
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
19 tháng 9 2016
Ta có f(x) đạt giá trị lớn nhất khi \(\frac{1}{f\left(x\right)}\) đạt giá trị nhỏ nhất.
Xét \(\frac{1}{f\left(x\right)}=\frac{x^2+2014x+1}{x}=x+\frac{1}{x}+2014\ge2\sqrt{x.\frac{1}{x}}+2014=2016\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}x>0\\x=\frac{1}{x}\end{cases}}\Leftrightarrow x=1\)
\(Min\)\(\frac{1}{f\left(x\right)}=2016\Leftrightarrow x=1\)
Vậy \(Max\)\(f\left(x\right)=\frac{1}{2016}\Leftrightarrow x=1\)
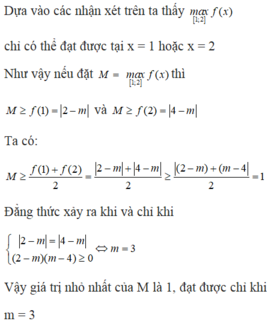
\(f\left(x\right)=2x+\frac{4}{x}\ge2\sqrt{\frac{8x}{x}}=4\sqrt{2}\)
\(f\left(x\right)_{min}=4\sqrt{2}\) khi \(x=\frac{2}{x}\Rightarrow x=\sqrt{2}\)