cho hàm số (c) có y=f(x) = x2-2x+3. viết phương trình tiếp tuyến với (c):
a) tại điểm thuộc (c) có hoành độ x0=1
b) song song với đường thẳng 4x-2y+5=0
c)vuông góc với đường thẳng x+4y=0
d)vuông góc với đường phân giác thứ nhất của góc hợp bởi các trục tọa độ


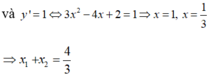
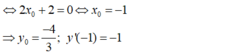
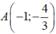 là:
là: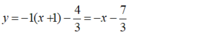
\(f'\left(x\right)=2x-2\)
a/ \(f'\left(1\right)=0\) ; \(f\left(1\right)=2\)
Phương trình tiếp tuyến: \(y=2\)
b/ \(4x-2y+5=0\Leftrightarrow y=2x+\frac{5}{2}\)
Tiếp tuyến song song d nên có hệ số góc bằng 2
\(\Rightarrow2x_0-2=2\Rightarrow x_0=2\)
\(f\left(2\right)=3\)
Pt tiếp tuyến: \(y=2\left(x-2\right)+3=0\Leftrightarrow y=2x-1\)
c/ \(x+4y=0\Rightarrow y=-\frac{1}{4}x\)
Tiếp tuyến vuông góc d \(\Rightarrow\) có hsg k thỏa mãn \(k.\left(-\frac{1}{4}\right)=-1\Rightarrow k=4\)
\(\Rightarrow2x_0-2=4\Rightarrow x_0=3\) ; \(f\left(3\right)=6\)
Pt tiếp tuyến: \(y=3\left(x-3\right)+6=3x-3\)
d/ Đường phân giác góc phần thứ thứ nhất có pt \(y=x\)
\(\Rightarrow\) Tiếp tuyến có hệ số góc -1
\(\Rightarrow2x_0-2=-1\Rightarrow x_0=\frac{1}{2}\) ; \(f\left(\frac{1}{2}\right)=\frac{9}{4}\)
Pt: \(y=-1\left(x-\frac{1}{2}\right)+\frac{9}{4}=-x+\frac{11}{4}\)