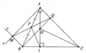
Cho tam giác ABC nhọn, từ A kẻ tia Ax song song với BC, từ C kẻ Cy song song với AB. Ax cắt Cy tại D. Gọi H, K là hình chiếu của B và D trên AC, Gọi O là trung điểm của AC.
a, Chứng minh ΔABC = ΔCDA
b, Chứng minh BH = DK, BK // HD
c, Chứng minh O là trung điểm của BD.
d, ΔABC cần thêm điều kiên gì để BD ⊥ AC.