1 f(x) là một nguyên hàm của hàm số f(x)=1/2x-1 biết f(1)=2 . tính f(2)
2 cho hàm số f(x) liên tục trên R và F(x) là nguyên hàm của f(x) biết \(\int_0^9\) f(x)dx=9 và f(0)=3. tính f(9)
3 biết f(x) là một nguyên hàm của hàm số f(x) =1/2x+1 và f(0)=1. tính giá trị f(2)
4 diện tích hình phẳng giới hạn bởi đồ thị hàm số y=xe^x , trúc hoành và hai đường thẳng x=-2, x=3 có công thức là
5 diện tích hình phẳng giới hạn bởi đồ thị hàm số y=-x^2 +4 , trục hoành và các đường thẳng x=0,x=3 là
6 diện tích giới hạn bởi đường thẳng x=0,x=\(\pi\) đồ thị hàm số cosx và trục ox la
7 công thức tính diện tích hình phẳng giới hạn bởi đồ thị y=f(x) trục ox và hai đường thẳng x=a, x=b (a<b) là
8diện tích hình phẳng giới hạn bởi đồ thị hàm số y =x^2+3 và y=4x là
9 ính diện tích hình phẳng giới hạn bởi y=-x^2+2x;y=-3x
10 diện tích hình phẳng giới hạn bởi hai đường hảng x=0,x=\(\pi\) , đồ thị hàm số y=cosx và trục ox là
11 gọi S là diện tích hình phẳng giới hạn bởi các đường y=x^3,y=2 và y=0 là
12 tính thể tích V của vật ròn xoay tạo thành khi quay hình phẳng (h) giới hạn bởi các đường y=x^2;y=\(\sqrt{x}\) quanh trục ox
13 cho phần vậy thể B giới hạn bởi hai mặt phẳng có phương trình x=0, x-\(\frac{\pi}{3}\)cắt phần vật thể B bởi mặ phẳng vuông góc trục ox tại điểm có hoành độ x(0\(\le x\le\frac{\pi}{3}\) ta được thiết diện là mộ tam giác vuông có độ dài hai cạnh lần lượt là 2x và cosx. thể tích vật thể B là
14 thể tích V của vật thể nằm giữa hai mặt phẳng x=0 , x= \(\pi\) biết rằng thiết diện của vật có thể bị cắt bởi mặt phẳng vuông góc trục ox tại điểm có hoành độ x \(0\le x\le1\) được thiết diện là hình vuông có cạnh (x+1)
15 Tính thể tích của vật thể nằm giữa hai mặt phẳng x=−1x=−1 và x=1x=1, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục OxOx có hoành độ x(−1≤x≤1)x(−1≤x≤1) là một tam giác vuông cân với cạnh 2\(\sqrt{1-x^2}\) thể tích vật thể là
16 cho hai số phức z=a+bi ,\(z^,\)=c+di. hai số phức z=\(z^,\) khi
a {a=c, bi=di} B {a=d,b=c} C {a=c,b=d} D(a=b,c=d}
17cho số phức z=3-2i tim phẩn ảo của số phức liên hợp z
18 cho số phức z= 3+2i . tìm phần thực của số phức z^2
19 cho hai số phức z=1+3i ,w=2-i tim phẩn ảo của số phức u=\(\overline{z}\) .w
20 trong mặt phẳng oxy, cho điểm A(4,0),B(1;4) và C(1;-1) . GỌI G là trọng tâm tam giác ABC . Biết rằng G là biểm biểu diễn số phức z là
A z=3+3/2i B=3-3/2i C z=2-i D z=2+i
21 cho số phức thỏa (1-i)+4\(4\overline{z}\) =7-7i .Mô đun của số phức z là

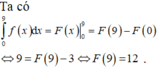
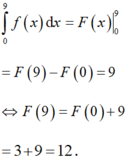
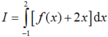
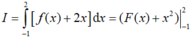


19.
\(\overline{z}=1-3i\)
\(\Rightarrow u=\left(1-3i\right)\left(2-i\right)=2+3i^2-7i=-1-7i\)
Phần ảo bằng -7
20.
Tọa độ G: \(\left\{{}\begin{matrix}x_G=\frac{x_A+x_B+x_C}{3}=2\\y_G=\frac{y_A+y_B+y_C}{3}=1\end{matrix}\right.\)
Biểu diễn trên mặt phẳng phức: \(z=2+i\)
21.
Đề đúng là \(\left(1-i\right)+44\overline{z}=7-7i\) chứ?
\(\Rightarrow44\overline{z}=6-6i\Rightarrow\overline{z}=\frac{3}{22}-\frac{3}{22}i\)
\(\Rightarrow z=\frac{3}{22}+\frac{3}{22}i\Rightarrow\left|z\right|=\sqrt{\left(\frac{3}{22}\right)^2+\left(\frac{3}{22}\right)^2}=\frac{3\sqrt{2}}{22}\)
15.
Diện tích thiết diện:
\(S=\frac{1}{2}\left(2\sqrt{1-x^2}\right)^2=2\left(1-x^2\right)=2-2x^2\)
Thể tích:
\(S=\int\limits^1_{-1}\left(2-2x^2\right)dx=\frac{8}{3}\)
16.
\(z=z'\Leftrightarrow\left\{{}\begin{matrix}a=c\\b=d\end{matrix}\right.\) (phần thực bằng phần thực, phần ảo bằng phần ảo)
17.
\(\overline{z}=3+2i\Rightarrow\) phần ảo là 2 (không phải 2i đâu)
18.
\(z=3+2i\Rightarrow z^2=\left(3+2i\right)^2=9+4i^2+12i=5+12i\)
\(\Rightarrow\) phần thực bằng 5