Viết phường trình đường thẳng (D1) song song (D) y=2x và tiếp xúc với (P)=y=\(-x^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KQ
0
HP
31 tháng 5 2021
1.
\(\left(C\right):x^2+y^2-2x-4=0\)
\(\Leftrightarrow\left(x-1\right)^2+y^2=5\)
Đường tròn \(\left(C\right)\) có tâm \(I=\left(1;0\right)\), bán kính \(R=\sqrt{5}\)
Phương trình đường thẳng \(d_1\) có dạng: \(x+y+m=0\left(m\in R\right)\)
Mà \(d_1\) tiếp xúc với \(\left(C\right)\Rightarrow d\left(I;d_1\right)=\dfrac{\left|1+m\right|}{\sqrt{2}}=\sqrt{5}\)
\(\Leftrightarrow\left|m+1\right|=\sqrt{10}\)
\(\Leftrightarrow m=-1\pm\sqrt{10}\)
\(\Rightarrow\left[{}\begin{matrix}d_1:x+y-1+\sqrt{10}=0\\d_1:x+y-1-\sqrt{10}=0\end{matrix}\right.\)
HP
31 tháng 5 2021
2.
Phương trình đường thẳng \(\Delta\) có dạng: \(x-y+m=0\left(m\in R\right)\)
Ta có: \(d\left(I;\Delta\right)=\sqrt{R^2-\dfrac{MN^2}{4}}=2\)
\(\Leftrightarrow\dfrac{\left|m+1\right|}{\sqrt{2}}=2\)
\(\Leftrightarrow m=-1\pm2\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:x-y+1+2\sqrt{2}=0\\\Delta:x-y+1-2\sqrt{2}=0\end{matrix}\right.\)
29 tháng 8 2023
a: (d) vuông góc (d1)
=>a*(-1/2)=-1
=>a=2
=>(d): y=2x+b
Thay x=-2 và y=5 vào (d), ta được:
b-4=5
=>b=9
b:
Sửa đề: (d1): y=-3x+4
Tọa độ giao của (d2) và (d3) là:
3x-7/2=2x-3 và y=2x-3
=>x=1/2 và y=1-3=-2
(d)//(d1)
=>(d): y=-3x+b
Thay x=1/2 và y=-2 vào (d), ta được:
b-3/2=-2
=>b=1/2
=>y=-3x+1/2
13 tháng 1 2022
Vì (d)//(d1) nên a=2
Vậy: (d): y=2x+b
Thay x=1 và y=4 vào (d), ta được:
b+2=4
hay b=2
CM
29 tháng 1 2017
Đáp án B
Mặt cầu S : x - 1 2 + y + 1 2 + z 2 = 11 có tâm I(1;-1;0) bán kính R= 11
Các đường thẳng d 1 , d 2 có vectơ chỉ phương lần lượt là:
Mặt phẳng α song song với d 1 , d 2 có vectơ pháp tuyến là:
α có dạng: α : 3x-y-z+d=0. Vì α tiếp xúc với (S ) nên: d(I; α )=R
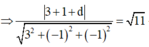
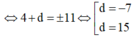
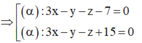
Nhận thấy điểm A(5;-1;1) ∈ d 1 cũng thuộc vào mặt phẳng 3x-y-z+15=0 =>mặt phẳng này chứa d 1
Vậy phương trình mặt phẳng α thỏa mãn yêu cầu bài toán là: α : 3x-y-z+7=0
vì D1 song song vs D
=> D1 = 2x + b
xét pt hoành độ giao điểm ta có
-x^2 = 2x +b <=> x^2 + 2x + b = 0
xét đen ta của phương trình trên ta đc: 4-4b
mà D1 tiếp xúc vs P Nên 4 - 4b = 0 => b=1
vậy đg thẳng D1 có dạng y= 2x+1