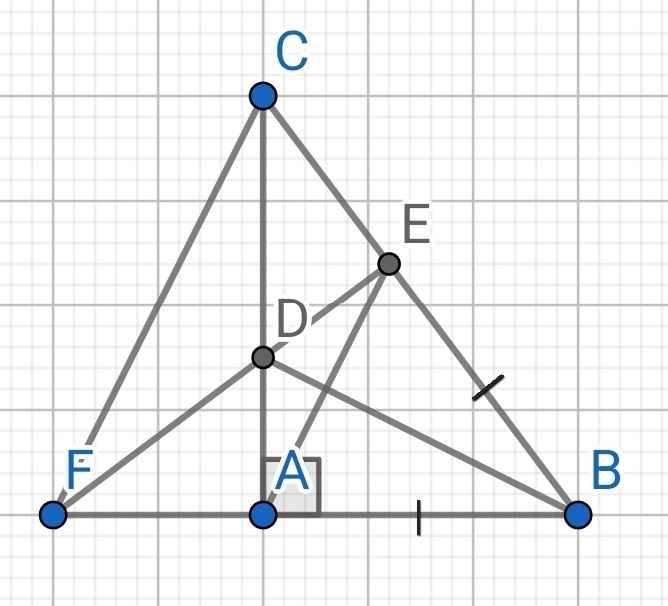
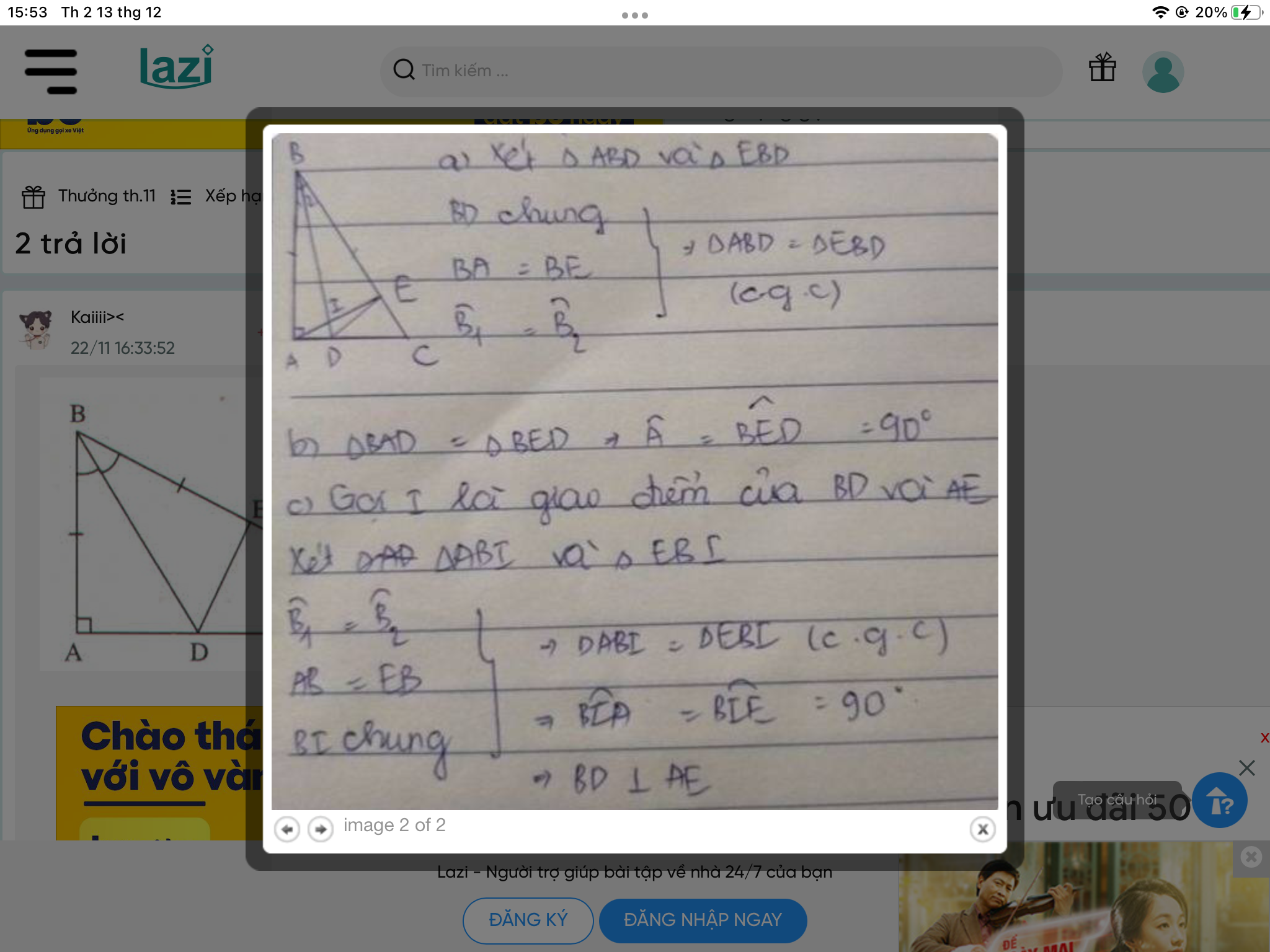
Cho tam giác ABC vuông tại A.Trên cạnh BC lấy điểm E sao cho BE = BA. Tia phân giác của góc B cắt AE tại I và cắt AC tại D
Gọi F là giao điểm của hai đường thẳng ED và AB.Chứng minh: FD = DC
Ai biết giải nhanh giùm mình nha, mình đang cần gấp, hãy giải chi tiếp giùm và nếu có thể hãy vẽ hình nha. Ai nhanh và chi tiết mình sẽ tích cho.


Nguyễn Khắc Vinh ko biết gì đâu! chỉ toàn trả lời vậy xin l-i-k-e thôi ak
bạn ghi gì thế,mình bảo chứng minh mà