Cho hình thang ABCD có A= B=90 độ, AB=AD. CD=BC+AD. BC<AD. E là trung điểm của AD. CM: góc ADC = 2 góc ABE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2,\)
Kẻ BH vuông góc với CD tại H
Xét hai tam giác BDH và BCH:
+) BH là cạnh chung
+) Góc BHD = góc BHC = 90 độ
+) DH = CH
=> Tam giác BDH = tam giác HCH (c.g.c)
=> BD = BC
Khác: DC = BC
=> BC = CD = DB => Tam giác BCD đều => Góc C = 60 độ
Mà: AB // CD => Góc B + góc C = 180 độ => Góc B = góc ABC = 180 độ - 60 độ = 120 độ

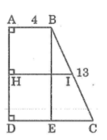
Kẻ BE ⊥ CD
Suy ra tứ giác ABED là hình chữ nhật
Ta có: AD = BE
AB = DE = 4 (cm)
Suy ra: CE = CD – DE = 9 – 4 = 5 (cm)
Áp dụng định lí Pitago vào tam giác vuông BCE ta có :
B C 2 = B E 2 + C E 2
Suy ra : B E 2 = B C 2 - C E 2 = 13 2 - 5 2 = 144
BE = 12 (cm)
Vậy: AD = 12 (cm)

Từ C kẻ đường thẳng vuông góc vs AB tại H
Vì AD=DC (gt)
góc A=góc D=góc H=90°
=> ADCH là hình vuông
=> AH=4 cm => BH=AB-AH=3 cm
CH=AD=4cm
Áp dụng định lý py-ta-go vào ΔCHB ta có: HC^2+BH^2=BC^2
=>4^2+3^2=BC^2 => BC=5cm


