Lập phương trình đường tròn nội tiếp tam giác OAB với A(-8,0), B(0,6)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NP
1
PQ
0
CM
25 tháng 5 2018
Gọi I là tâm đường tròn ngoại tiếp ta tìm hai đường phân giác trong của tam giác rồi cho giao với nhau. (chú ý ở đây có kĩ thuật viết phương trình đường phân giác trong của tam giác trong không gian).
Đáp án cần chọn là A
CM
26 tháng 4 2017
Đáp án A.
Ta có O E E ∈ A B Vecto chỉ phương
của đường thẳng (d) là u → = 1 ; − 2 ; 2 .
Kẻ phân giác O E E ∈ A B suy ra
O A O B = A E B E = 3 4 ⇒ A E → = 3 4 E B → ⇒ E 0 ; 12 7 ; 12 7 .
Gọi I là tâm đường tròn nội tiếp
Δ O A B ⇒ I ∈ O E ⇒ O I → = k O E , → với k > 0.
Tam giác OAB vuông tại O, có bán kính
đường tròn nội tiếp r = 1 ⇒ I O = 2 .
Mà
A E = 15 7 ; O A = 3 ; c os O A B ^ = 3 5 → O E = 12 2 7 s u y r a O E ¯ = 12 7 O I ¯ ⇒ I 0 ; 1 ; 1 .
Vậy phương trình đường thẳng cần tìm là
d : x + 1 1 = y − 3 − 2 = z + 1 2
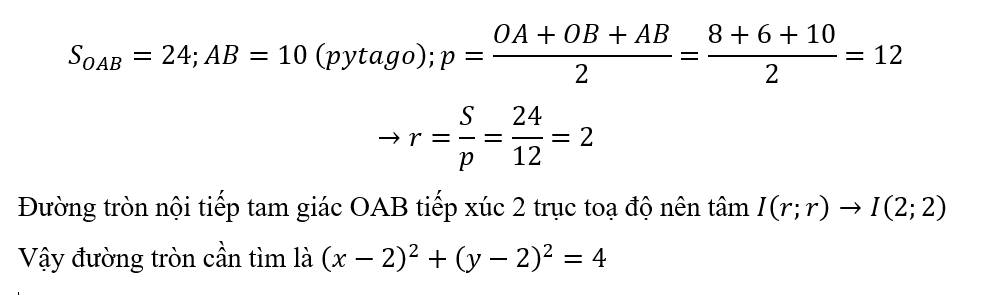
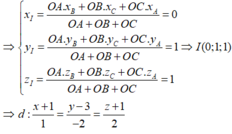
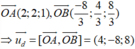
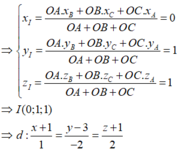
\(\overrightarrow{AB}=\left(8;6\right)=2\left(4;3\right)\)
Phương trình AB:
\(3\left(x+8\right)-4\left(y-0\right)=0\Leftrightarrow3x-4y+24=0\)
Đường thẳng OA trùng với trục Ox nên có pt \(y=0\)
Đường thẳng OB trùng với trục Oy nên có pt \(x=0\)
Gọi \(I\left(a;b\right)\) là tâm đường tròn nội tiếp
\(\Leftrightarrow\left\{{}\begin{matrix}d\left(I;OA\right)=d\left(I;AB\right)\\d\left(I;OA\right)=d\left(I;OB\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{\left|3a-4b+24\right|}{\sqrt{3^2+4^2}}=\left|b\right|\\\left|a\right|=\left|b\right|\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left|3a-4b+24\right|=\left|5b\right|\\\left|a\right|=\left|b\right|\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=2\end{matrix}\right.\) \(\Rightarrow I\left(-2;2\right)\Rightarrow d\left(I;OA\right)=2=R\)
Pt đường tròn:
\(\left(x+2\right)^2+\left(y-2\right)^2=4\)
tại sao từ chỗ \(\left\{{}\begin{matrix}\left|3a-4b+24\right|=\left|5b\right|\\\left|a\right|=\left|b\right|\end{matrix}\right.\) tại suy ra được a = -2 và b = 2 ạ? em làm chi tiết đoạn đó ra nhiều trường hợp lắm ạ, làm sao để loại trường hợp đi ạ?