cho tam giác ABC vuông tại A, có BC = 6cm, B = 60' (60 độ, k ghi đc dấu độ:"<) . Hãy giải tam giác ABC (giúp bn e đang kt với ạ)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, BA = BD (gt)
=> Δ ABD cân tại B (đn)
góc ABC = 60 (gt)
=> Δ ABD đều (dấu hiệu)
b) Ta có\(\widehat{A}\)=90 độ và\(\widehat{B}\)=60 độ =>\(\widehat{C}\)=30 độ (1)
Mà BI là phân giác của \(\widehat{B}\)=> \(\widehat{IBC}\)=30 độ(2)
từ (1) và (2) => Δ IBC cân tại I
c) xét 2 tam giác BIA và BID có: \(\widehat{A}\)+\(\widehat{AIB}\)+\(\widehat{IBA}\)+\(\widehat{IBD}\)+\(\widehat{BDI}\)+\(\widehat{DIB}\)=360 độ
=> \(\widehat{AID}\)=120 độ
=> \(\widehat{DIC}\)=60 độ
Xét Δ BIA và Δ CID có:
DI=AI (Δ BIA=Δ BID)
\(\widehat{BIA}\)=\(\widehat{DIC}\)=60 độ
IB=IC(vìΔ IBC cân)
=>ΔBIA=Δ CID(c.g.c)
=> BA=CD mà BA=BD=> BD=DC
=> D là trung điểm của BC
d) vì AB=\(\dfrac{1}{2}\) BC nên BC=12 cm
Áp dụng định lí py-ta-go ta có:
BC2=AB2+AC2
=> AC2=BC2−AB2
=> AC2=144 - 36=108 cm
=> AC= \(\sqrt{108}\)(cm)
vậy BC=12 cm; AC= \(\sqrt{108}\)cm

Xét ΔABC vuông tại A có sin C=AB/BC
=>6/BC=1/2
=>BC=12cm
AC=căn 12^2-6^2=6*căn 3(cm)
AH=6*6căn 3/12=3*căn 3(cm)
BH=AB^2/BC=3cm
CH=12-3=9cm

Bài 1:
AC=4cm
Xét ΔABC có AB<AC
nên \(\widehat{C}< \widehat{B}\)
Bài 2:
BC=6cm
=>AB+AC=14cm
mà AB=AC
nên AB=AC=7cm
Xét ΔABC có AB=AC>BC
nên \(\widehat{B}=\widehat{C}>\widehat{A}\)
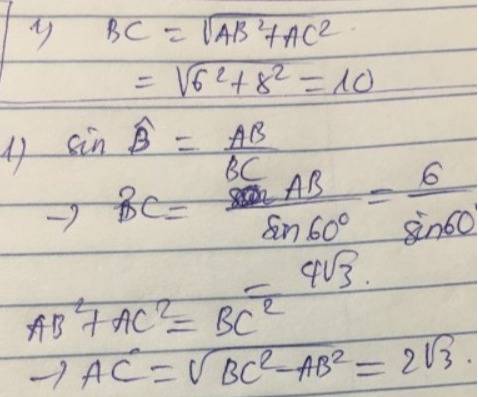

\(sinB=\dfrac{AC}{BC}\Rightarrow AC=sin60^0.6=3\sqrt{3}\left(cm\right)\)
\(AB=\sqrt{BC^2-AC^2}=\sqrt{6^2-\left(3\sqrt{3}\right)^2}=3\left(cm\right)\)
\(\widehat{C}=90^0-\widehat{B}=90^0-60^0=30^0\)
ΔABC vuông tại A có:
sinB=\(\dfrac{AC}{BC}=\dfrac{AC}{6}\)⇒AC=sin60.6=\(3\sqrt{3}cm\)
cosb=\(\dfrac{AB}{BC}=\dfrac{AB}{6}\)⇒AB=cos60.6=3cm
góc C = 90-góc B=90-30=60 độ