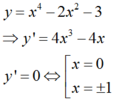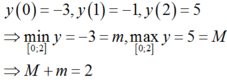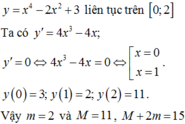Tìm giá trị lớn/nhỏ nhất của biểu thức 2x2-14x+3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
3 tháng 3 2019
2 x 2 + 10 - 1 = 2 x 2 + 5 x - 1 / 2 B = 2 x 2 + 2 . 5 / 2 x + 5 / 2 2 - 5 / 2 2 - 1 / 2 = 2 x + 5 / 2 2 - 25 / 4 - 2 / 4 = 2 x + 5 / 2 2 - 27 / 2 = 2 x + 5 / 2 2 - 27 / 2 V ì x + 5 / 2 2 ≥ 0 n ê n 2 x + 5 / 2 2 ≥ 0 ⇒ 2 x + 5 / 2 2 - 27 / 2 ≥ - 27 / 2
Suy ra: B ≥ - 27/2 .
B= -27/2 khi và chỉ khi x + 5/2 = 0 suy ra x = -5/2
Vậy B = -27/2 là giá trị nhỏ nhất tại x = - 5/2
21 tháng 7 2023
=2(x^2-5/2x+3/2)
=2(x^2-2*x*5/4+25/16-1/16)
=2(x-5/4)^2-1/8>=-1/8
Dấu = xảy ra khi x=5/4
23 tháng 10 2021
Bài 4:
\(A=2x^2-15\ge-15\\ A_{min}=-15\Leftrightarrow x=0\\ B=2\left(x+1\right)^2-17\ge-17\\ B_{min}=-17\Leftrightarrow x=-1\)
Bài 5:
\(A=-x^2+14\le14\\ A_{max}=14\Leftrightarrow x=0\\ B=25-\left(x-2\right)^2\le25\\ B_{max}=25\Leftrightarrow x=2\)
23 tháng 10 2021
mik chưa học giá trị lớn nhất là max và giá trị nhỏ nhất là min nên bạn cho mik kí hiệu khác nha
PT
1
CM
30 tháng 7 2018
A = 2 x 2 - 8 x - 10
= 2 x 2 - 4 x + 4 - 18 = 2 x - 2 2 - 18
Do 2 x - 2 2 ≥ 0 với mọi x ⇒ 2 x - 2 2 – 18 ≥ −18
A = -18 khi và chỉ khi x - 2 = 0 hay x = 2
Do đó giá trị nhỏ nhất của biểu thức A bằng -18 tại x = 2
H9
HT.Phong (9A5)
CTVHS
19 tháng 8 2023
Tìm giá trị nhỏ nhất của biểu thức:
a) Ta có:
\(M=2x^2+4x+7\)
\(M=2\cdot\left(x^2+2x+\dfrac{7}{2}\right)\)
\(M=2\cdot\left(x^2+2x+1+\dfrac{5}{2}\right)\)
\(M=2\cdot\left[\left(x+1\right)^2+2,5\right]\)
\(M=2\left(x+1\right)^2+5\)
Mà: \(2\left(x+1\right)^2\ge0\forall x\) nên:
\(M=2\left(x+1\right)^2+5\ge5\forall x\)
Dấu "=" xảy ra:
\(2\left(x+1\right)^2+5=5\Leftrightarrow2\left(x+1\right)^2=0\)
\(\Leftrightarrow\left(x+1\right)^2=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
Vậy: \(M_{min}=5\) khi \(x=-1\)
b) Ta có:
\(N=x^2-x+1\)
\(N=x^2-2\cdot\dfrac{1}{2}\cdot x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(N=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà: \(\left(x+\dfrac{1}{2}\right)^2\ge0\forall x\) nên \(N=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=" xảy ra:
\(\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=\dfrac{3}{4}\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=0\)
\(\Leftrightarrow x-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{2}\)
Vậy: \(N_{min}=\dfrac{3}{4}\) khi \(x=\dfrac{1}{2}\)
H9
HT.Phong (9A5)
CTVHS
19 tháng 8 2023
Tìm giá trị lớn nhất của biểu thức
a) Ta có:
\(E=-4x^2+x-1\)
\(E=-\left(4x^2-x+1\right)\)
\(E=-\left[\left(2x\right)^2-2\cdot2x\cdot\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{15}{16}\right]\)
\(E=-\left[\left(2x-\dfrac{1}{4}\right)^2+\dfrac{15}{16}\right]\)
Mà: \(\left(2x+\dfrac{1}{4}\right)^2+\dfrac{15}{16}\ge\dfrac{15}{16}\forall x\) nên
\(\Rightarrow E=-\left[\left(2x+\dfrac{1}{4}\right)^2+\dfrac{15}{16}\right]\le-\dfrac{15}{16}\forall x\)
Dấu "=" xảy ra:
\(-\left[\left(2x+\dfrac{1}{4}\right)^2+\dfrac{15}{16}\right]=-\dfrac{15}{16}\Leftrightarrow-\left(2x+\dfrac{1}{4}\right)^2-\dfrac{15}{16}=-\dfrac{15}{16}\)
\(\Leftrightarrow-\left(2x+\dfrac{1}{4}\right)^2=0\Leftrightarrow2x-\dfrac{1}{4}=0\Leftrightarrow x=\dfrac{1}{16}\)
Vậy: \(E_{max}=-\dfrac{15}{16}\) khi \(x=\dfrac{1}{16}\)
b) Ta có:
\(F=5x-3x^2+6\)
\(F=-3x^2+5x-6\)
\(F=-\left(3x^2-5x-6\right)\)
\(F=-3\left(x^2-\dfrac{5}{3}x-2\right)\)
\(F=-3\left[\left(x-\dfrac{5}{6}\right)^2-\dfrac{97}{36}\right]\)
\(F=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{36}\)
Mà: \(-3\left(x-\dfrac{5}{6}\right)^2\le0\forall x\) nên:
\(F=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{36}\le\dfrac{97}{36}\forall x\)
Dấu "=" xảy ra:
\(-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{36}=\dfrac{97}{36}\Leftrightarrow-3\left(x-\dfrac{5}{6}\right)^2=0\)
\(\Leftrightarrow x-\dfrac{5}{6}=0\Leftrightarrow x=\dfrac{5}{6}\)
Vậy: \(F_{max}=\dfrac{97}{36}\) khi \(x=\dfrac{5}{6}\)
9 tháng 7 2021
Bài 3:
a) Ta có: \(A=25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3>0\forall x\)(đpcm)
d) Ta có: \(D=x^2-2x+2\)
\(=x^2-2x+1+1\)
\(=\left(x-1\right)^2+1>0\forall x\)(đpcm)
9 tháng 7 2021
Bài 1:
a) Ta có: \(A=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
DN
0