Xét dấu
g(x) = -6x3 - 19x2 - 11x+6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 8 2021
a: \(\dfrac{2x^3-5x^2-x+1}{2x+1}\)
\(=\dfrac{2x^3+x^2-6x^2-3x+2x+1}{2x+1}\)
\(=x^2-3x+1\)
b: \(\dfrac{x^3-2x+4}{x+2}\)
\(=\dfrac{x^3+2x^2-2x^2-4x+2x+4}{x+2}\)
\(=x^2-2x+2\)
HN
1
10 tháng 3 2022
\(f\left(x\right)=\dfrac{11x+3}{-x^2+5x-7}.\)
Ta có: \(-x^2+5x-7\) là 1 tam thức bậc 2.
\(\left\{{}\begin{matrix}a=-1< 0.\\\Delta=5^2-4.\left(-1\right).\left(-7\right)=-3< 0.\end{matrix}\right.\)
\(\Rightarrow-x^2+5x-7>0\forall x\in R.\)
\(\Rightarrow\) \(f\left(x\right)>0.\Leftrightarrow11x+3>0.\Leftrightarrow x>\dfrac{-3}{11}.\\ f\left(x\right)< 0.\Leftrightarrow11x+3>0.\Leftrightarrow x>\dfrac{-3}{11}.\\ f\left(x\right)=0.\Leftrightarrow x=\dfrac{-3}{11}.\)
8 tháng 8 2021
c) Ta có: \(C=4x^2+y^2-4xy+8x-4y+4\)
\(=\left(2x-y\right)^2+2\cdot\left(2x-y\right)\cdot2+2^2\)
\(=\left(2x-y+2\right)^2\)
HH
24 tháng 6 2018
Giải:
a) \(x^3-6x^2+11x-6=0\)
\(\Leftrightarrow x^3-3.x^2.2+3.x.2^2-x-2^3+2=0\)
\(\Leftrightarrow x^3-3.x^2.2+3.x.2^2-2^3+2-x=0\)
\(\Leftrightarrow\left(x-2\right)^3+2-x=0\)
\(\Leftrightarrow\left(x-2\right)^3-\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(\left(x-2\right)^2-1\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-2-1\right)\left(x-2+1\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\\x=1\end{matrix}\right.\)
Vậy ...
b) \(x+\left|2x-1\right|=5\)
\(\Leftrightarrow\left|2x-1\right|=5-x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=5-x\\2x-1=x-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=6\\x=-4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)
Vậy ...
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) \(f\left( x \right) = 6{x^2} + 41x + 44\) có \(\Delta = 625 > 0\), có hai nghiệm phân biệt là \({x_1} = - \frac{{11}}{2},{x_2} = - \frac{4}{3}\) và có \(a = 6 > 0\)
Ta có bảng xét dấu \(f\left( x \right)\)như sau:
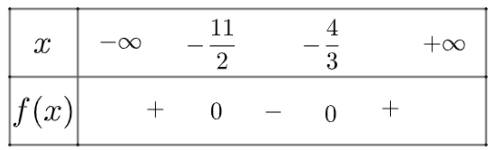
Vậy \(f\left( x \right)\) dương trong khoảng \(\left( { - \infty ; - \frac{{11}}{2}} \right) \cup \left( { - \frac{4}{3}; + \infty } \right)\) và âm trong khoảng \(\left( { - \frac{{11}}{2}; - \frac{4}{3}} \right)\)
b) \(g\left( x \right) = - 3{x^2} + x - 1\) có \(\Delta = - 11 < 0\) và có \(a = - 3 < 0\)
Ta có bảng xét dấu như sau
Vậy \(g\left( x \right)\)luôn âm với mọi \(x \in \mathbb{R}\)
c) \(h\left( x \right) = 9{x^2} + 12x + 4\) có \(\Delta = 0\), có nghiệm kép là \({x_1} = {x_2} = - \frac{2}{3}\) và có \(a = 9 > 0\)
Ta có bảng xét dấu của \(h\left( x \right)\) như sau:
Vậy \(h\left( x \right)\) luôn dương khi \(x \ne - \frac{2}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2021
1.
\(f\left(x\right)=2x^4+6x^3+8x^2+12x+1\)
2.
\(h\left(x\right)=\left(2x^4+6x^3+8x^2+12x+1\right)-\left(2x^4+6x^3+17x^2+12x-26\right)\)
\(=-9x^2+27\)
3.
\(h\left(x\right)=0\Leftrightarrow-9x^2+27=0\)
\(\Leftrightarrow x^2=3\Rightarrow x=\pm\sqrt{3}\)
\(g\left(x\right)=\left(x+2\right)\left(1-3x\right)\left(2x+3\right)\)
\(g\left(x\right)=0\) khi \(\left[{}\begin{matrix}x=-2\\x=-\frac{3}{2}\\x=\frac{1}{3}\end{matrix}\right.\)
\(g\left(x\right)>0\) khi \(\left[{}\begin{matrix}x< -2\\-\frac{3}{2}< x< \frac{1}{3}\end{matrix}\right.\)
\(g\left(x\right)< 0\) khi \(\left[{}\begin{matrix}-2< x< -\frac{3}{2}\\x>\frac{1}{3}\end{matrix}\right.\)