Tính bằng cách thuận tiện nhất:
0,63 x 8 + 0,63 + 0,63 + 9,89
Giải nhanh giúp mik với ạ, mik đang cần gấp. Cảm ơn rất nhiều!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
28 tháng 4 2020
a) 0,63 x 8 + 0,63 + 0,63 x 9,89
= 0.63 x ( 8+1+9.89 ) = 0.63 x 18.98 = 11.9
b) 9,89 x 99 + 9,89
= 9.89 x ( 99 + 1) = 9.89 x 100 = 989
28 tháng 4 2020
a) 0,63 x 8 + 0,63 + 0,63 x 9,89
= 0,63 x 8 + 0,63 x 1 + 0,63 x 9,89
= 0,63 x ( 8 + 1 + 9,89 )
= 0,63 x 18,89
= 11,9007
b) 9,89 x 99 + 9,89
= 9,89 x 99 + 9,89 x 1
= 9,89 x ( 99 + 1 )
= 9,89 x 100
= 989
28 tháng 4 2020
a)0,63 x 8 +0,63+ 0,63x 9,89
=0,63 x 8+0,63 x 1 +0,63 x 9,89
=0,63 x(8+1+9,89)
= 0,63 x 18,89
= 11,9001
b)9,89+99 x 9,89
=9,89x1+99x 9,89
=9,89 x(99+1)
=9,89 x 100
=989
k mk nha,chúc bn hok tốt!!!!!!!!
19 tháng 4 2023
= ( 2380 + 9 x 480) : 25 - 3500 : 25
= ( 2380 + 4320 - 3500 ) : 25
= 3200 : 25
= 128
HD
6
CC
20 tháng 11 2018
\(\text{0, 37 + 5 , 684 + 3, 2 + 0 , 63 + 5 , 8 + 4 , 316}\)
\(=\left(0,37+0,63\right)+\left(5,684+4,316\right)+\left(3,2+5,8\right)\)
\(=\text{}\text{}1+10+9\)
\(=20\)
T
1
SA
14 tháng 6 2021
\(A=\dfrac{4x+2\sqrt{x}+2}{2\sqrt{x}+1}=\dfrac{2\sqrt{x}\left(2\sqrt{x}+1\right)+2}{2\sqrt{x}+1}=2\sqrt{x}+\dfrac{2}{2\sqrt{x}+1}\)
\(=2\sqrt{x}+1+\dfrac{2}{2\sqrt{x}+1}-1\ge2\sqrt{\left(2\sqrt{x}+1\right)\cdot\dfrac{2}{2\sqrt{x}+1}}-1=2\sqrt{2}-1\)
=> A \(\ge2\sqrt{2}-1\)
Dấu "=" xảy ra <=> \(2\sqrt{x}+1=\dfrac{2}{2\sqrt{x}+1}\)
<=> \(\left(2\sqrt{x}+1\right)^2=2\) <=> \(\left[{}\begin{matrix}2\sqrt{x}+1=2\\2\sqrt{x}+1=-2\left(loại\right)\end{matrix}\right.\)
<=> \(\sqrt{x}=\dfrac{1}{2}\) <=> \(x=\dfrac{1}{4}\)(tm)
Vậy minA = \(2\sqrt{2}-1\) khi x = 1/4
18 tháng 9 2023
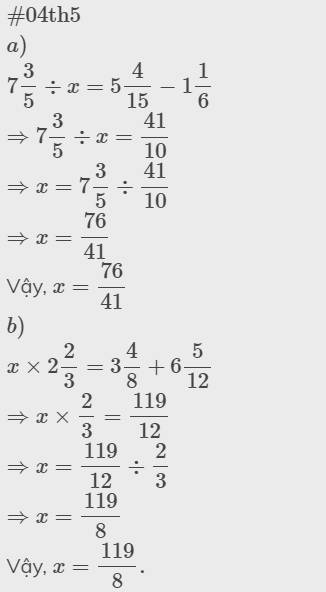
Mình nhớ câu này mình đã giải rồi, không biết vì lý do gì mà bạn lại xóa đi vậy nhỉ? Và nếu CH đã đăng, yêu cầu bạn không đăng lại lần thứ 2!
0,63 x 8 + 0,63 + 0,63 + 9,89
=0,63 x 8 + 0,63 x 1 + 0,63 x1 + 9,89
= 0,63 x ( 8+ 1 + 1 ) +9,89
= 0,63 x 10 +9,89
= 6,3 +9,89
= 16,19