Chứng minh rằng : a2 + b2 + c2 + \(\dfrac{3}{4}\)≥ a + b + c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1/a+1/b+1/c=0
=>(ab+ac+bc)/abc=0
=> ab+ac+bc=0
(a+b+c)^2=a^2+b^2+c^2+2(ab+ac+bc)=0
=> a^2+b^2+c^2=0
Bạn xem lại đề nhé.

Ta chứng minh BĐT sau:
\(\dfrac{1}{x^3+x+2}\ge\dfrac{-x^2+3}{8}\) với \(x>0\)
Thật vậy, BĐT tương đương:
\(\left(x^2-3\right)\left(x^3+x+2\right)+8\ge0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x^3+2x^2+x+2\right)\ge0\) (luôn đúng)
Áp dụng:
\(\Rightarrow VT\ge\dfrac{-a^2+3}{8}+\dfrac{-b^2+3}{8}+\dfrac{-c^2+3}{8}=\dfrac{9-\left(a^2+b^2+c^2\right)}{8}=\dfrac{3}{4}\)
Dấu "=" xảy ra khi \(a=b=c=1\)

Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
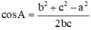
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.

Tham khảo:
https://hoc24.vn/cau-hoi/cho-a-b-c-la-do-dai-ba-canh-cua-mot-tam-giac-va-thoa-man-he-thuc-a-b-c-1-cmr-a2-b2-c2-12.139261258302

a) \(\dfrac{a^2+a+1}{a^2-a+1}=\dfrac{\left(a+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}{\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\)
Thấy tử và mẫu của phân số đều lớn hơn 0 => \(\dfrac{a^2+a+1}{a^2-a+1}>0\)
b)\(a^2+b^2+c^2+3\ge2\left(a+b+c\right)\)
\(\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2-2a+1\right)+\left(c^2-2a+1\right)\ge0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\) (luôn đúng với mọi a,b,c)
Dấu = xra khi a=b=c=1
b)
\(a^2-2a+1+b^2-2b+1+c^2-2c+1\ge0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\) ( Luôn đúng)
Dấu "=" xảy ra khi a=b=c=1
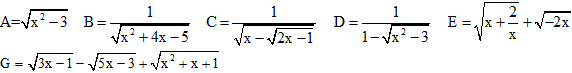 Mn giúp em với ;-;
Mn giúp em với ;-;