Xác định tọa độ đỉnh P của parabol y=3(x-2)^2+0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 12 2019
Ở đây a = 2; b = -2; c = -2. Ta có Δ = ( - 1 ) 2 - 4 . 2 . ( - 2 ) = 17
Trục đối xứng là đường thẳng x = 1/4; đỉnh I(1/4; -17/8) giao với trục tung tại điểm (0; -2).
Để tìm giao điểm với trục hoành ta giải phương trình
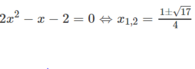
Vậy các giao điểm với trục hoành là
CM
26 tháng 6 2019
Trục đối xứng x = -1/4; đỉnh I(-1/4; -17/8) giao với trục tung tại điểm (0;2); giao với trục hoành tại các điểm
28 tháng 1 2023
a: Trục đối xứng là x=-(-1)/4=1/4
Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{1}{4}\\y=-\dfrac{\left(-1\right)^2-4\cdot2\cdot\left(-2\right)}{4\cdot2}=-\dfrac{17}{8}\end{matrix}\right.\)
Thay y=0 vào (P), ta được:
2x^2-x-2=0
=>\(x=\dfrac{1\pm\sqrt{17}}{4}\)
thay x=0 vào (P), ta được:
y=2*0^2-0-2=-2
b: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-\left(-6\right)}{2\cdot\left(-3\right)}=\dfrac{6}{-6}=-1\\y=-\dfrac{\left(-6\right)^2-4\cdot\left(-3\right)\cdot4}{4\cdot\left(-3\right)}=7\end{matrix}\right.\)
=>Trục đối xứng là x=-1
Thay y=0 vào (P), ta được:
-3x^2-6x+4=0
=>3x^2+6x-4=0
=>\(x=\dfrac{-3\pm\sqrt{21}}{3}\)
Thay x=0 vào (P), ta được:
y=-3*0^2-6*0+4=4
c: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-\left(-1\right)}{2\cdot\left(-2\right)}=\dfrac{1}{-4}=\dfrac{-1}{4}\\y=-\dfrac{\left(-1\right)^2-4\cdot\left(-2\right)\cdot2}{4\cdot\left(-2\right)}=\dfrac{17}{8}\end{matrix}\right.\)
=>Trục đối xứng là x=-1/4
Thay y=0 vào (P), ta được:
-2x^2-x+2=0
=>2x^2+x-2=0
=>\(x=\dfrac{-1\pm\sqrt{17}}{4}\)
Thay x=0 vào (P), ta được:
y=-2*0^2-0+2=2
CM
26 tháng 8 2018
y = x2 – 3x + 2 có a = 1 ; b = –3 ; c = 2 ; Δ = b2 – 4ac = (–3)2 – 4.2.1 = 1.
+ Đỉnh của Parabol là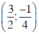 
+ Khi x = 0 thì y = 2. Vậy giao điểm với trục tung là A(0 ; 2).
+ Khi y = 0 thì x2 – 3x + 2 = 0. Phương trình có hai nghiệm x = 2 hoặc x = 1.
Vậy giao điểm với trục hoành là B(2 ; 0) và C(1 ; 0).
PT
1
CM
10 tháng 5 2019
Parabol y = ax2 + bx + c có:
+ Tọa độ đỉnh D là:
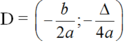
+ Phương trình trục đối xứng là:
CM
24 tháng 3 2017
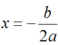
y = –2x2 + 4x – 3 có a = –2 ; b = 4 ; c = –3 ; Δ= b2 – 4ac = 42 – 4.( –3).( –2) = –8
+ Đỉnh của Parabol là (1 ; –1).
+ Khi x = 0 thì y = –3. Vậy giao điểm với trục tung là A(0 ; –3).
+ Khi y = 0 thì –2x2 + 4x – 3 = 0. Phương trình vô nghiệm.
Vậy Parabol không cắt trục hoành.
khi m thay đổi
x2 và đường thẳng (d) : y = mx - 
.
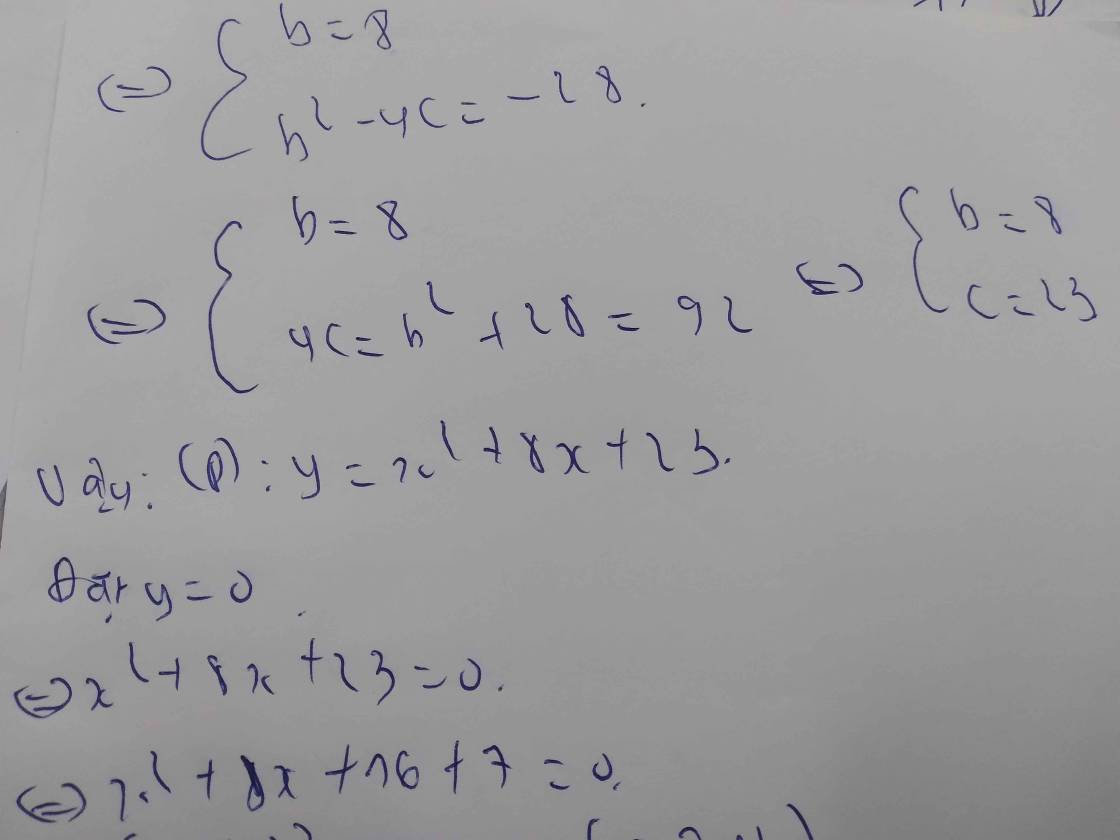
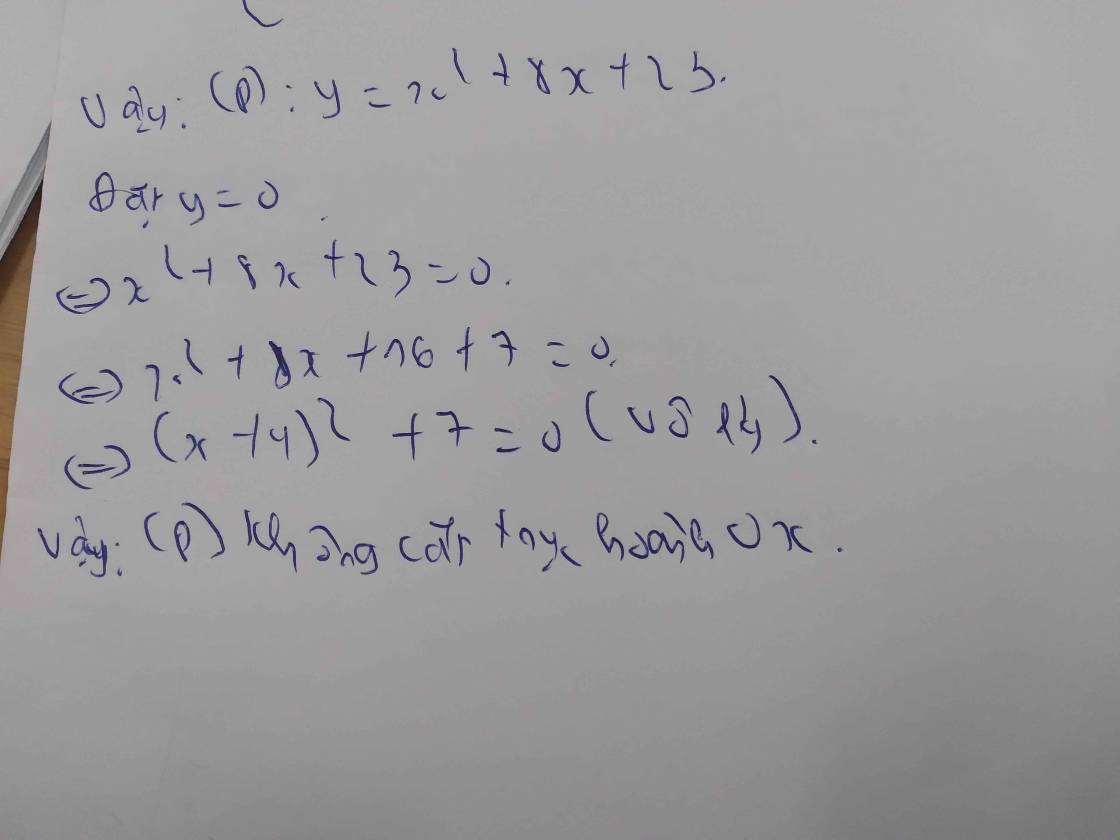
Lời giải:
$y=3x^2-12+12$
Tọa độ đỉnh $P$: \((\frac{-b}{2a}, \frac{4ac-b^2}{4a})=(\frac{12}{2.3}, \frac{4.3.12-12^2}{4.3})=(2,0)\)