chứng tỏ bất phương trình: x2-2x+17<3-4x vô nghiệm
Giúp mình với ạ!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tham khảo câu hỏi của đắng sôcôla trên hoc24.vn nha

Ta có :
\(x^2-4x+5=\left(x^2-2.2x+2^2\right)+1=\left(x-2\right)^2+1\ge1>0\)
Vậy đa thức \(x^2-4x+5\) vô nghiệm với mọi giá trị của x
Chúc bạn học tốt ~

pt <=> x^4+x^3+x^2+x^2+x+1=0
<=> x^4+x^2+x^3+x+x^2+1=0
<=> x^2(x^2+1)+x(x^2+1)+(x^2+1)=0
<=>(x^2+x+1)(x^2+1)=0
<=> x^2+x+1=0 (Vô nghiệm)
hoặc x^2+1=0 (vô lý)
=>pt vô nghiệm
tk mk nhé

\(a,x^2+2x+2=\left(x+1\right)^2+1\ge1>0\)
\(=>bpt:x^2+2x+2\le0\left(vo-li\right)\)
=>bpt vô nghiệm
\(b,4x^2-4x+5=\left(2x-1\right)^2+4\ge4>0\)
\(=>bpt:4x^2-4x+5\le0\left(vo-li\right)\)
=>bpt vô nghiệm
a, \(< =>x^2+2x+1+1\le0\)
\(< =>\left(x+1\right)^2+1\le0\) vô nghiệm với mọi x thuộc R
b, \(< =>\left(2x-1\right)^2+4\le0\)vô nghiệm với mọi x thuộc R

Điều kiện xác định x ≥ –8
Ta có: 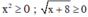 nên
nên 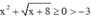 với mọi x ≥ –8.
với mọi x ≥ –8.
Do đó BPT 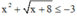 vô nghiệm.
vô nghiệm.

Vì 2x^2-6x > 0 với mọi x
=> 2x^2-6x+2020 > 0+2020 với mọi x
=> 2x^2-6x+2020 > 2020 với mọi x
=> A(x) > 0 ( khác 0 )
=> A(x) vô nghiệm

1.
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=\left(m+1\right)^2-4m\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-3m^2+7m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow m< \dfrac{7-\sqrt{61}}{6}\)
2.
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\3m^2+13m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4\le m\le-\dfrac{1}{3}\end{matrix}\right.\)
Không tồn tại m thỏa mãn
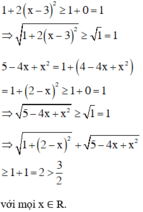
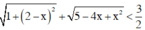 vô nghiệm.
vô nghiệm.
Vì x^2-2x+17<3-4x←→x^2+2x+14<0←→(x+1)^2+13<0←→Vô nghiệm
Ta có: \(x^2-2x+17< 3-4x\)
\(\Leftrightarrow x^2-2x+17-3+4x< 0\)
\(\Leftrightarrow x^2+2x+14< 0\)(1)
Ta có: \(x^2+2x+14\)
\(=x^2+2x+1+13\)
\(=\left(x+1\right)^2+13\)
Ta có: \(\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+1\right)^2+13\ge13>0\forall x\)
hay \(x^2+2x+14>0\forall x\)(2)
Từ (1) và (2) suy ra \(x\in\varnothing\)
hay bất phương trình \(x^2-2x+17< 3-4x\) vô nghiệm(đpcm)