Cho tứ giác MNPQ nội tiếp nửa đường tròn đk MQ. Gọi I là giao điểm của MP với NQ. Kẻ IH vuông góc với MQ
a)Cm MNIH;PQHI là tứ giác nội tiếp
b) cm NQ la pg của góc PNH
c) Gọi K là trung điểm của IQ.cm PNKH nội tiếp
d) Cm MN,PQ,IH đồng quy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 5 2019
a/ Ta có
IH vuông góc AB => ^AHI = 90
IK vuông góc AD => ^AKI = 90
=> H và K cùng nhìn AI dưới hai góc bằng nhau => AHIK là tứ giác nội tiếp
b/ Xét tam giác ADI và tam giác BCI có
^AID=^BIC (góc đối đỉnh)
sđ ^DAC = sđ ^DBC = 1/2 sđ cung CD (góc nội tiếp) => ^DAC=^DBC
=> tg ADI đồng dạng tg BCI
=>\(\frac{IA}{IB}=\frac{ID}{IC}\)⇒IA.IC=IB.ID
c/
Xét tứ giác nội tiếp AHIK có
^HIK = 180 - ^DAB (hai góc đối của tứ giác nội tiếp bù nhau) (1)
^DAC = ^KHI (2 góc nội tiếp chắn cùng 1 cung) (2)
Xét tứ giác nội tiếp ABCD có
^BCD = 180 - ^DAB (hai góc đối của tứ giác nội tiếp bù nhau) (3)
^DAC = ^DBC (hai góc nội tiếp chắn cùng 1 cung) (4)
Xét hai tam giác HIK và tam giác BCD
Từ (1) và (3) => ^HIK = ^BCD
Từ (2) và (4) => ^KHI = ^DBC
=> tam giác HIK đồng dạng với tam giác BCD
24 tháng 5 2023
c: AHIK nội tiếp
=>góc AIK=góc AHK
BHKC nội tiếp nên góc ICK=góc AHK
=>góc ICK=góc AIK
=>góc AIC=90 độ
Hình vẽ đoạn thẳng A,K mình vẽ hơi xấu
NB
18 tháng 3 2017
1) Vì một tam giác vuông luôn nội tiếp đường tròn đường kính = cạnh huyền
\(\Rightarrow\)Tam giác vuông BHF và tam giác BDH nội tiếp đường tròn đường kính BH
\(\Leftrightarrow\)4 điểm B,F,H,D cùng nằm trên đường tròn \(\Rightarrow\)Tứ giác BFHD nội tiếp đường tròn đường kính BH
17 tháng 6 2017
a,TỨ GIÁC ĐẤY NT CM ĐC R NHA BN
b,bn cm thêm tứ giác HECD nt nứa xong suy ra góc HAE = HCE (1)
từ tứ giác ý a nt suy ra góc MDH =FBE (2)
TỨ giác EFBC nt suy ra góc FBE =FCE (3)
TỪ 1 2 VÀ 3 SUY RA DC LÀ PHÂN GIÁc
7 tháng 3 2021
a) Xét (O) có
ΔCAB nội tiếp đường tròn(C,A,B∈(O))
AB là đường kính(gt)
Do đó: ΔCAB vuông tại C(Định lí)
⇔\(\widehat{ACB}=90^0\)
hay \(\widehat{KCB}=90^0\)
Xét tứ giác BHKC có
\(\widehat{BHK}\) và \(\widehat{KCB}\) là hai góc đối
\(\widehat{BHK}+\widehat{KCB}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BHKC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
NN
25 tháng 11 2018
a) Xét tam giác QMN có :
A là trung điểm của MN
B là trung điểm của MQ
=) AB là đường trung bình của tam giác QMN
=) AB // MQ Và AB=\(\frac{1}{2}\)MQ (*)
Xét tam giác QPN có :
C là trung điểm của QP
D là trung điểm của NP
=) CD là đường trung bình của tam giác QPN
=) CD // QN Và CD=\(\frac{1}{2}\)QN (**)
Từ (*) và (**) =) Tứ giác ABCD là hình bình hành (1)
Xét tam giác MQP có :
B là trung điểm của MQ
C là trung điểm của QP
=) BC là đường trung bình của tam giác MQP
=) BC // MP
Do MNPQ là hình thoi =) MP\(\perp\)NQ
Mà BC // MP và AB // NQ
=) BC\(\perp\)AB (2)
Từ (1) và (2) =) ABCD là hình chữ nhật
b) Ta có : MQ=QP
Do B là trung điểm của MQ =) MB=BQ=\(\frac{MQ}{2}\)
Do C là trung điểm của QP =) QC=CP=\(\frac{QP}{2}\)
=) QB=QC
Do MNPQ là hình thoi =) QM là đường phân giác \(\widehat{MQP}\)
=) \(\widehat{MQN}\)=\(\widehat{NQP}\)=\(\frac{\widehat{MQP}}{2}\)
Xét tam giác QMN có:
MQ=MQ và \(\widehat{QMN}\)=600
=) QMN là tam giác đều
Xét tam giác MQN có :
NQ là đường trung tuyến=) NQ là đường phân giác của \(\widehat{MNQ}\)
=) \(\widehat{MNB}\)=\(\widehat{BNQ}\)=\(\frac{\widehat{MNQ}}{2}\)=\(\frac{60^0}{2}\)= 300
Xét tam giác QBN và tam giác QCN có :
QB=QC ( chứng minh trên )
\(\widehat{BQN}\)=\(\widehat{CQN}\) ( chứng minh trên )
QN là cạch chung
=) tam giác QBN = tam giác QCN (c-g-c)
=)\(\widehat{BNQ}\)=\(\widehat{QNC}\) =300 (2 góc tương ứng ) và BN=CN ( 2 cạch tương ứng )
=) Tam giác BNC là tam giác cân tại N (3)
Ta có : \(\widehat{BNQ}\)+\(\widehat{QNC}\)=\(\widehat{BNC}\)
=) 300 +300 =\(\widehat{BNC}\)
=) \(\widehat{BNC}\)=600 (4)
Từ (3) và (4) =) Tam giác BNC là tam giác đều
CM
19 tháng 1 2018
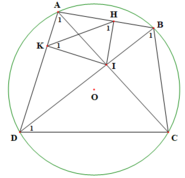
a) Tứ giác AHIK có:
A H I ^ = 90 0 ( I H ⊥ A B ) A K I ^ = 90 0 ( I K ⊥ A D ) ⇒ A H I ^ + A K I ^ = 180 0
=> Tứ giác AHIK nội tiếp.
b) ∆ IAD và ∆ IBC có:
A ^ 1 = B ^ 1 (2 góc nội tiếp cùng chắn cung DC của (O))
A I D ^ = B I C ^ (2 góc đối đỉnh)
=> ∆ IAD ~ ∆ IBC (g.g)
⇒ I A I B = I D I C ⇒ I A . I C = I B . I D
c, Xét đường tròn ngoại tiếp tứ giác AHIK có K ^ 1 = D ^ 1
A ^ 1 = H ^ 1 (2 góc nội tiếp cùng chắn cung IK)
mà A ^ 1 = B ^ 1 ⇒ H ^ 1 = B ^ 1
Chứng minh tương tự, ta được K ^ 1 = D ^ 1
∆ HIK và ∆ BCD có: H ^ 1 = B ^ 1 ; K ^ 1 = D ^ 1
=> ∆ HIK ~ ∆ BCD (g.g)
d) Gọi S1 là diện tích của ∆ BCD.
Vì ∆ HIK ~ ∆ BCD nên:
S ' S 1 = H K 2 B D 2 = H K 2 ( I B + I D ) 2 ≤ H K 2 4 I B . I D = H K 2 4 I A . I C (1)
Vẽ A E ⊥ B D , C F ⊥ B D ⇒ A E / / C F ⇒ C F A E = I C I A
∆ ABD và ∆ BCD có chung cạnh đáy BD nên:
S 1 S = C F A E ⇒ S 1 S = I C I A (2)
Từ (1) và (2) suy ra
S ' S 1 ⋅ S 1 S ≤ H K 2 4 I A . I C ⋅ I C I A ⇔ S ' S ≤ H K 2 4 I A 2 (đpcm)
HAI GÓC VĨ T