Cho hình chóp đều S. ABCD. Gọi E là điểm đối xứng với D qua trung điểm của SA; M, N lần lượt là trung điểm AE và BC. Tính góc giữa MN và BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 12 2018
Chọn B.
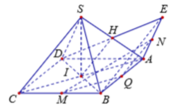
Gọi H = DF ∩ SA => H là trung điểm của ED. I = AC ∩ BD => I là trung điểm BD
Vậy HI là đường trung bình của tam giác BED => HI//EB(1)
Ta có 
(chóp tứ giác đều, hình chiếu của đỉnh S xuống đáy là I)
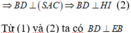
Gọi Q à trung điểm AB; dễ thấy NQ là đường trung bình của tam giác ABE => NQ//BE.
Gọi M là trung điểm BC; dễ thấy MQ//AC , 
Ta có 
Góc giữa hai đường thẳng MN và BD bằng 90 °
CM
18 tháng 1 2018
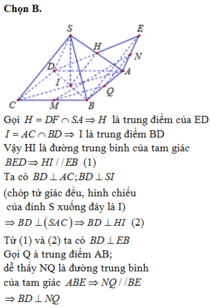
Chọn đáp án D
Gọi I là trung điểm của SA. Khi đó I cũng là trung điểm của ED.
Vậy góc giữa hai đường thẳng MN và BD bằng 90 °
CM
19 tháng 12 2017
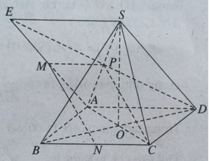
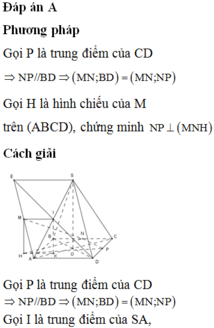
Gọi P là trung điểm SA, ta có MPCN là hình bình hành.
Như vậy MN // PC, suy ra MN // (SAC).
Do BD ⊥ (SAC) nên BD ⊥ MN.
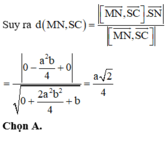
Ta có: d(MN, AC) = d(N, (SAC))
Mà C ∈(SAC) & CN/CB = 1/2
Nên d(N, (SAC)) = 1/2 d(B, (SAC)) = 1/2 BO (O là giao điểm của AC và BD).
Vậy d(N, (SAC)) = 1/4a√2.
CM
9 tháng 12 2018
Phương pháp:
- Gắn hệ tọa độ Oxyz với O là tâm hình vuông đáy,
- Xác định tọa độ các điểm cần thiết và tính khoảng cách.
Cách giải:
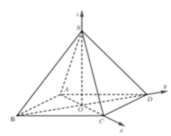
Gắn hệ trục tọa độ như hình vẽ, giả sử SO = b ta có:
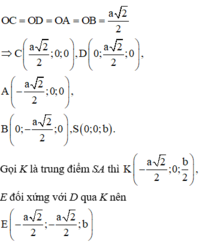
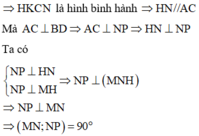
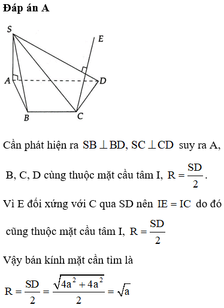
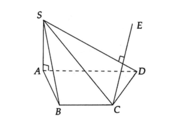
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Tứ giác SDAE là hbh (hai đường chéo cắt nhau tại trung điểm)
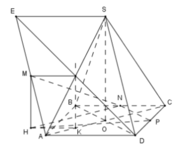
Gọi H là hình chiếu của E trên (ABCD)
\(\left\{{}\begin{matrix}SE=AD\\SE//AD\end{matrix}\right.\) \(\Rightarrow H\) đối xứng O qua AB
Gọi K là hình chiếu của M lên (ABCD)
\(\Rightarrow\) K là trung điểm AH
Tứ giác AOBH là hbh (2 đường chéo cắt nhau tại trung điểm)
\(\Rightarrow AH//BD\)
Gọi P là trung điểm AB \(\Rightarrow KP//OA\) (đường trung bình)
Mà \(KN//AC\) (đường trung bình)
\(\Rightarrow K;P;N\) thẳng hàng
\(KN//AC\) ; \(AC\perp BD\Rightarrow KN\perp BD\)
\(\Rightarrow BD\perp\left(KMN\right)\Rightarrow BD\perp MN\)