Cho 1 lượng HCl dư vào hỗn hợp chứa 25 gam hai muối NaClO và CaOCl2 , sau phản ứng xảy ra hoàn toàn, thu được 5,60 lít khí (đktc) dung dịch A. Cô cạn dung dịch A thu được m gam chất rắn khan. Giá trị của m là?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án D
Ta có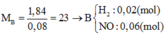
Vì khí B có H2 nên trog dung dịch muối sẽ không có ion NO3-
Ta có
![]()
![]()
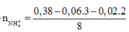
=0,02
![]()
Vậy trong muối có

=>m=29(g)

Câu 1 :\(n_{CO_2} = \dfrac{2,688}{22,4} = 0,12(mol)\)
MgCO3 + 2HCl \(\to\) MgCl2 + CO2 + H2O
..................................0,12........0,12..................(mol)
Suy ra: a = 0,12.95 = 11,4(gam)
Câu 2 :
\(Fe + 2HCl \to FeCl_2 + H_2\\ n_{Fe} = n_{H_2} = \dfrac{3,36}{22,4} = 0,15(mol)\\ \Rightarrow n_{Cu} = 2n_{Fe} = 0,15.2 = 0,3(mol)\\ 2Fe+3Cl_2\xrightarrow{t^o} 2FeCl_3\\ Cu+Cl_2 \xrightarrow{t^o} CuCl_2\\ n_{Cl_2} = \dfrac{3}{2}n_{Fe} + n_{Cu} = 0,525\\ \Rightarrow V = 0,525.22,4 =11,76(lít)\)

Đáp án A
Phương pháp:
BTNT H: nHCl pư = 2nH2
BTKL: m + mHCl = m muối + mH2 =>m
Hướng dẫn giải:
BTNT H: nHCl pư = 2nH2 = 0,45 mol
BTKL: m + mHCl = m muối + mH2
=> m + 0,45.36,5 = 29,475 + 0,225.2
=> m = 13,5 gam

Đáp án A
Phương pháp:
BTNT H: nHCl pư = 2nH2
BTKL: m + mHCl = m muối + mH2 =>m
Hướng dẫn giải:
BTNT H: nHCl pư = 2nH2 = 0,45 mol
BTKL: m + mHCl = m muối + mH2 => m + 0,45.36,5 = 29,475 + 0,225.2 => m = 13,5 gam

Giải thích:
BTNT H: nHCl pư = 2nH2 = 0,45 mol
BTKL: m + mHCl = m muối + mH2 => m + 0,45.36,5 = 29,475 + 0,225.2 => m = 13,5 gam
Đáp án A
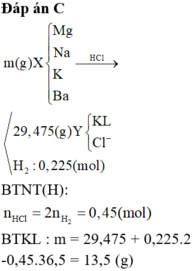

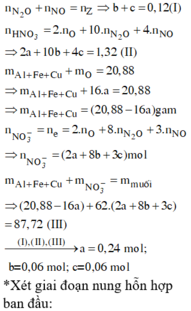
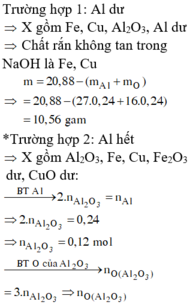
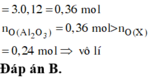
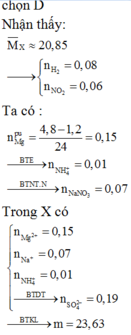
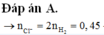
Gọi \(\left\{{}\begin{matrix}n_{NaClO}=a\left(mol\right)\\n_{CaOCl2}=b\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow74,5a+127b=25\left(1\right)\)
PTHH :
\(NaClO+2HCl\rightarrow NaCl+Cl_2+H_2O\)
a_________________________a _______
\(CaOCl_2+2HCl\rightarrow CaCl_2+Cl_2+H_2O\)
b _________________________ b__________
\(\Rightarrow n_{Cl2}=a+b=\frac{5,6}{22,4}=0,25\left(2\right)\)
\(\left(1\right)+\left(2\right)\Rightarrow\left\{{}\begin{matrix}a=\frac{9}{70}\\b=\frac{17}{140}\end{matrix}\right.\)
\(\Rightarrow m=m_{NaCl}+m_{CaCl2}=58,5.\frac{9}{70}+111.\frac{17}{140}=21\left(g\right)\)