Cho sin(40o+a)=a (0o<a<45o). Tính cos(70o+a)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
với 0o < a < 90o cho sin a = 3 cos a khi đó tính 4 - sina cosa tâ được kết quả là:
A.3
B.3,5
C.3,7
D.3,9
1
N
19 tháng 11 2021
\(\sin^2\alpha+\cos^2\alpha=1\Leftrightarrow10\cos^2\alpha=1\Leftrightarrow\cos\alpha=\sqrt{\dfrac{1}{10}}=\dfrac{\sqrt{10}}{10}\\ \Leftrightarrow\sin\alpha=\dfrac{3\sqrt{10}}{10}\\ \Leftrightarrow4-\sin\alpha\cdot\cos\alpha=4-\dfrac{\sqrt{10}\cdot3\sqrt{10}}{100}=4-\dfrac{3}{10}=3,7\)
Vậy chọn C
PT
1
CM
9 tháng 3 2018
Ta có: ΔABC = ΔDIK nên ∠A = ∠D; ∠B= ∠I ; ∠C = ∠K
Suy ra: ∠I = 50°; ∠C = 40°
Xét tam giác ABC ta có:
∠A + ∠B +∠C = 180° nên:
∠A = 180° –( ∠B+∠C) = 180° –(50° +40°) = 90°
Do đó: ∠A = 90°
CM
24 tháng 12 2017
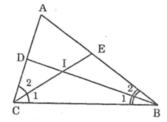
Ta có:
+ Trong ΔBIC có ∠BIC = 180º - (∠B1 + ∠C1) (1)
+ BI, CI là phân giác của ∠ABC và ∠BCA nên:
∠B1 = 1/2. ∠BAC; ∠C1 = 1/2. ∠ACB
⇒ ∠B1 + ∠C1 = 1/2. (∠BAC + ∠BCA) (2)
+ Trong ΔABC có: ∠BAC + ∠BCA = 180 - ∠A =140º (3).
Từ (1), (2) và (3) suy ra ∠BIC = 180º - 1/2.140º = 110º
Chọn đáp án C
CM
10 tháng 5 2018
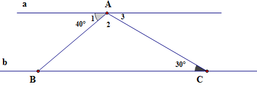
Ta có AI là tia phân giác của góc A nên ∠(BAI) = 40o:2=20o. Chọn A
CM
18 tháng 2 2017
Ta có AI là tia phân giác của góc A nên ∠(BAI) = 40o:2=20o. Chọn A
\(\alpha>0\Rightarrow\cos\left(40^0+\alpha\right)>0\Rightarrow\cos\left(40^0+\alpha\right)=\sqrt{1-\left[\sin^2\left(40^0+\alpha\right)\right]}=\sqrt{1-a^2}\)
\(\cos\left(70^0+\alpha\right)=\cos\left(30^0+40^0+\alpha\right)\)
\(=\cos30^0.\cos\left(40^0+\alpha\right)+\sin30^0.\sin\left(40^0+\alpha\right)\)
\(=\frac{\sqrt{3}}{2}.\sqrt{1-a^2}+\frac{1}{2}.a=\frac{1}{2}\left(\sqrt{3\left(1-a^2\right)}+a\right)\)