Giúp mình câu 18 với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 18:
PT: \(Zn+2HCl\rightarrow ZnCl_2+H_2\)
\(n_{Zn}=\dfrac{6,5}{65}=0,1\left(mol\right)\)
\(n_{HCl}=0,15.2=0,3\left(mol\right)\)
Xét tỉ lệ: \(\dfrac{0,1}{1}< \dfrac{0,3}{2}\), ta được HCl dư.
Theo PT: \(n_{ZnCl_2}=n_{H_2}=n_{Zn}=0,1\left(mol\right)\)
\(\Rightarrow V_{H_2}=0,1.22,4=2,24\left(l\right)\)
\(C_{M_{ZnCl_2}}=\dfrac{0,1}{0,15}=\dfrac{2}{3}\left(M\right)\)

17.
Gọi số vi khuẩn ban đầu là x
Sau 5 phút số vi khuẩn là: \(x.2^5=64000\Rightarrow x=2000\)
Sau k phút:
\(2000.2^k=2048000\Rightarrow2^k=1024=2^{10}\)
\(\Rightarrow k=10\)
18.
\(S_{2019}=\left(\dfrac{1}{2}\right)^1+1+\left(\dfrac{1}{2}\right)^2+1+...+\left(\dfrac{1}{2}\right)^{2019}+1\)
\(=\left(\dfrac{1}{2}\right)^1+\left(\dfrac{1}{2}\right)^2+...+\left(\dfrac{1}{2}\right)^{2019}+2019\)
Xét \(S=\left(\dfrac{1}{2}\right)^1+\left(\dfrac{1}{2}\right)^2+...+\left(\dfrac{1}{2}\right)^{2019}\) là tổng cấp số nhân với \(\left\{{}\begin{matrix}u_1=\dfrac{1}{2}\\q=\dfrac{1}{2}\\n=2019\end{matrix}\right.\)
\(\Rightarrow S=\dfrac{1}{2}.\dfrac{\left(\dfrac{1}{2}\right)^{2019}-1}{\dfrac{1}{2}-1}=1-\dfrac{1}{2^{2019}}\)
\(\Rightarrow S_{2020}=2019+S=2020-\dfrac{1}{2^{2019}}\)
19. C là khẳng định sai, ví dụ: \(u_n=2\) ; \(v_n=-\dfrac{1}{n}\)

17)
a)
\(CH_3-CH_3\underrightarrow{t^o,xt}CH_2=CH_2+H_2\)
\(CH_2=CH_2+Br_2\rightarrow CH_2Br-CH_2Br\)
\(CH_2Br-CH_2Br+2KOH\underrightarrow{ancol,t^o}CH\equiv CH+2KBr+2H_2O\)
\(CH\equiv CH+H_2O\underrightarrow{HgSO_4,H_2SO_4}CH_3CHO\)
b)
\(CaC_2+2H_2O\rightarrow Ca\left(OH\right)_2+CH\equiv CH\)
\(2CH\equiv CH\underrightarrow{đime.hóa}CH\equiv C-CH=CH_2\)
\(CH\equiv C-CH=CH_2+H_2\underrightarrow{t^o,Pd/PbCO_3}CH_2=CH-CH=CH_2\)
\(nCH_2=CH-CH=CH_2\underrightarrow{t^o,p,Na}\left(-CH_2-CH=CH-CH_2-\right)_n\)
c)
\(Al_4C_3+12H_2O\rightarrow4Al\left(OH\right)_3+3CH_4\)
\(2CH_4\underrightarrow{1500^oC,làm.lạnh.nhanh}CH\equiv CH+3H_2\)
\(CH\equiv CH+H_2\underrightarrow{t^o,Pd/PbCO_3}CH_2=CH_2\)
\(CH_2=CH_2+H_2O\underrightarrow{t^o,H_2SO_4}CH_3-CH_2OH\)
\(CH_3-CH_2OH+3O_2\underrightarrow{t^o}2CO_2+3H_2O\)
d)
\(CH_3-CH_2OH\underrightarrow{170^oC,H_2SO_4}CH_2=CH_2+H_2O\)
\(CH_2=CH_2+HCl\rightarrow CH_3-CH_2Cl\)
\(CH_3-CH_2Cl+KOH\underrightarrow{t^o,ancol}CH_2=CH_2+KCl+H_2O\)
\(nCH_2=CH_2\underrightarrow{t^o,p,xt}\left(-CH_2-CH_2-\right)_n\)
\(\)
18)
- Trích một ít các chất làm mẫu thử
a)
- Cho các khí tác dụng với dd AgNO3/NH3
+ Không hiện tượng: C2H6, C2H4 (1)
+ Kết tủa vàng: C2H2
\(C_2H_2+2AgNO_3+2NH_3\rightarrow C_2Ag_2+2NH_4NO_3\)
- Dẫn các khí còn lại ở (1) tác dụng với dd Br2 dư:
+ dd nhạt màu dần: C2H4
\(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
+ Không hiện tượng: C4H10
b)
- Dẫn các khí qua dd AgNO3/NH3:
+ Không hiện tượng: C4H10, \(CH_3-C\equiv C-CH_3\) (1)
+ Kết tủa vàng: \(CH\equiv C-CH_2-CH_3\)
\(CH\equiv C-CH_2-CH_3+AgNO_3+NH_3\rightarrow CAg\equiv C-CH_2-CH_3\downarrow+NH_4NO_3\)
- Dẫn các khí còn lại ở (1) tác dụng với dd Br2 dư
+ dd nhạt màu dần: \(CH_3-C\equiv C-CH_3\)
\(CH_3-C\equiv C-CH_3+2Br_2\rightarrow CH_3-CBr_2-CBr_2-CH_3\)
+ Không hiện tượng: C2H6
c)
- Dẫn các khí qua dd AgNO3/NH3:
+ Kết tủa vàng: \(CH\equiv C-CH_3\)
\(CH\equiv C-CH_3+AgNO_3+NH_3\rightarrow CAg\equiv C-CH_3\downarrow+NH_4NO_3\)
+ Không hiện tượng: C2H6, \(CH_2=CH-CH=CH_2\) (1)
- Dẫn các khí còn lại ở (1) tác dụng với dd Br2 dư
+ dd nhạt màu dần: \(CH_2=CH-CH=CH_2\)
\(CH_2=CH-CH=CH_2+2Br_2\rightarrow CH_2Br-CHBr-CHBr-CH_2Br\)
+ Không hiện tượng: C2H6


a.
\(\Delta=\left(2k-1\right)^2-4\left(2k-2\right)=4k^2-12k+9=\left(2k-3\right)^2\ge0;\forall k\)
\(\Rightarrow\) Phương trình luôn có nghiệm với mọi k
b.
Theo hệ thức Viet: \(x_1+x_2=2k-1\)

\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

Câu 5:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: Xét tứ giác AEDF có
\(\widehat{EAF}=\widehat{AFD}=\widehat{AED}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác của \(\widehat{FAE}\)
nên AEDF là hình vuông





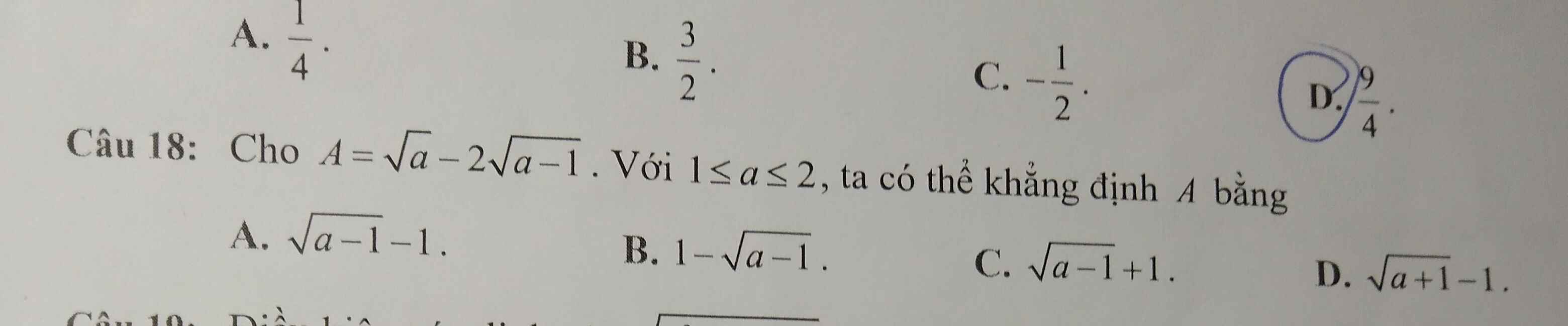


18.A
A