cho hình vẽ biết BC//EF a) chứng minh AD//EF b)Tính góc...
Đọc tiếp
cho hình vẽ biết BC//EF a) chứng minh AD//EF b)Tính góc BAE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VQ
1
Những câu hỏi liên quan
QH
0
QH
0
QH
2
24 tháng 10 2021
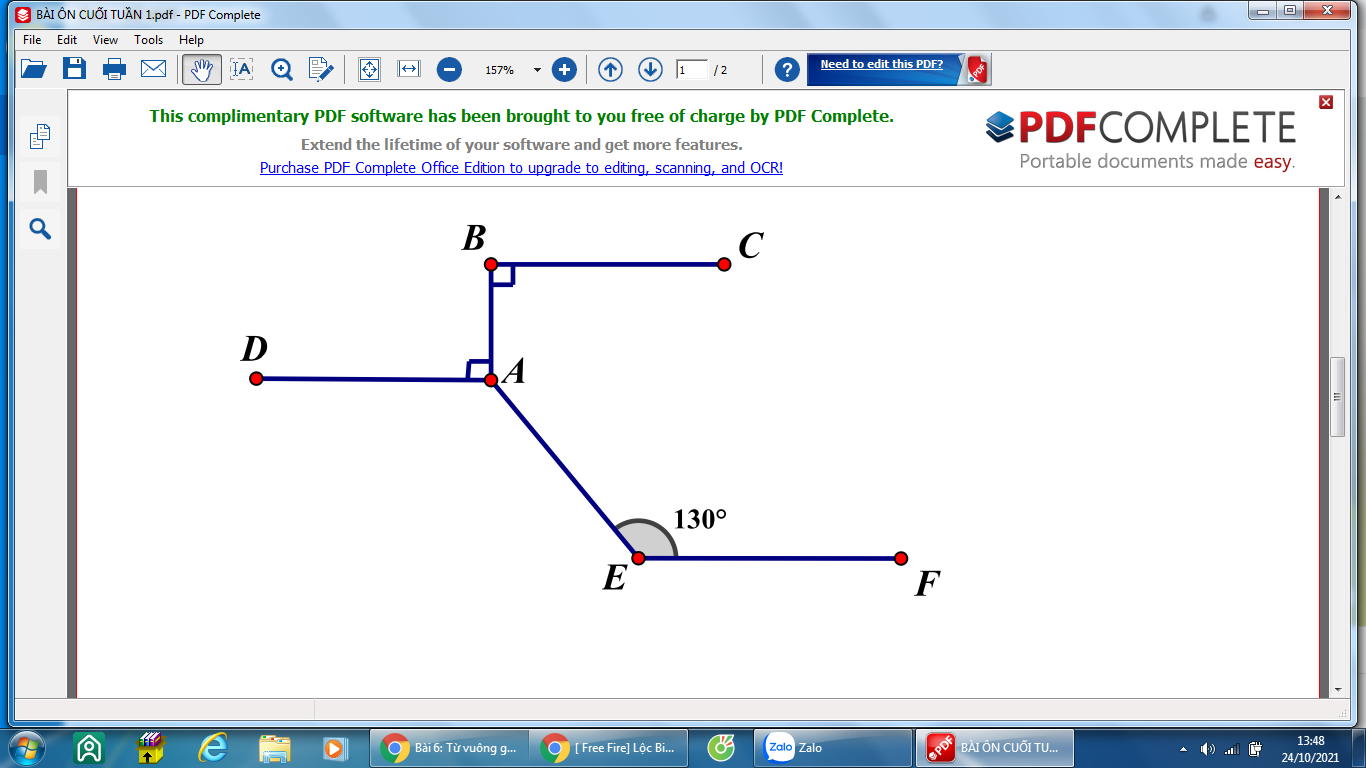
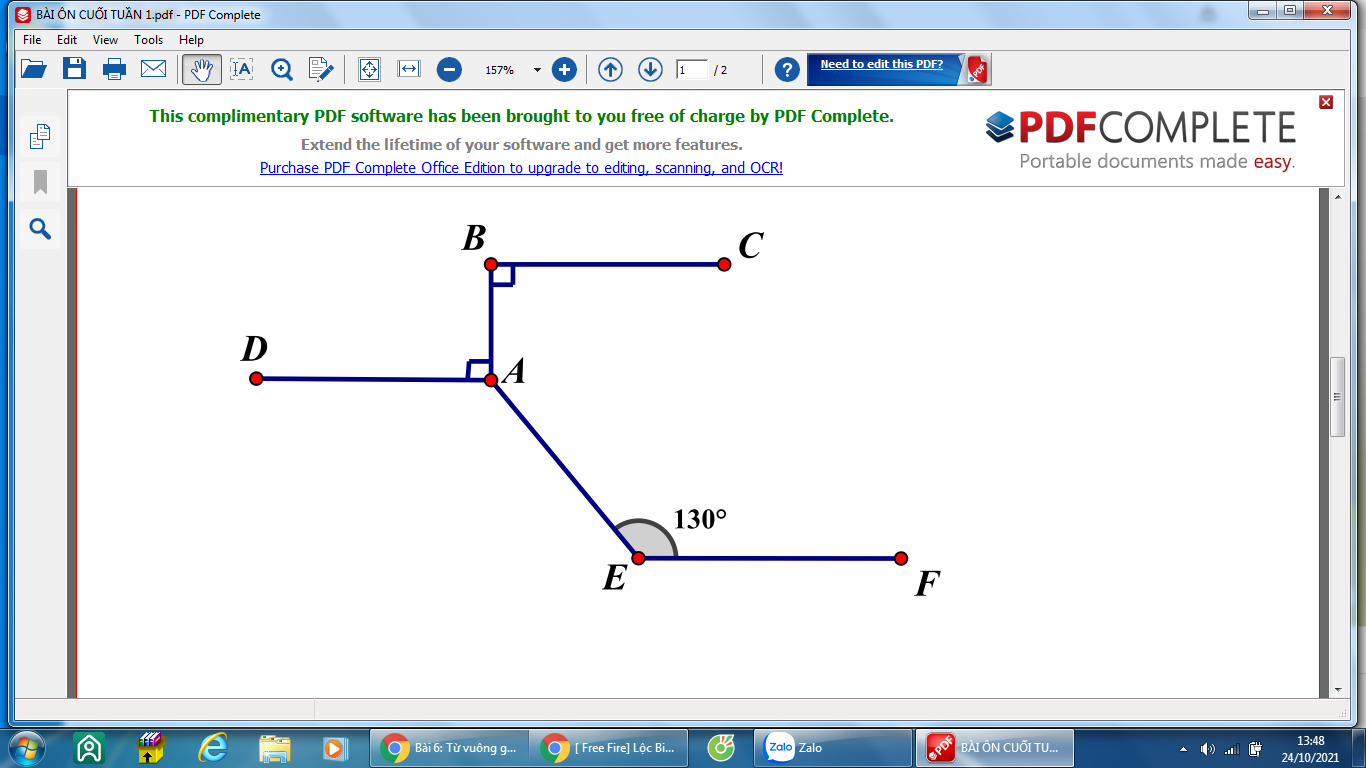
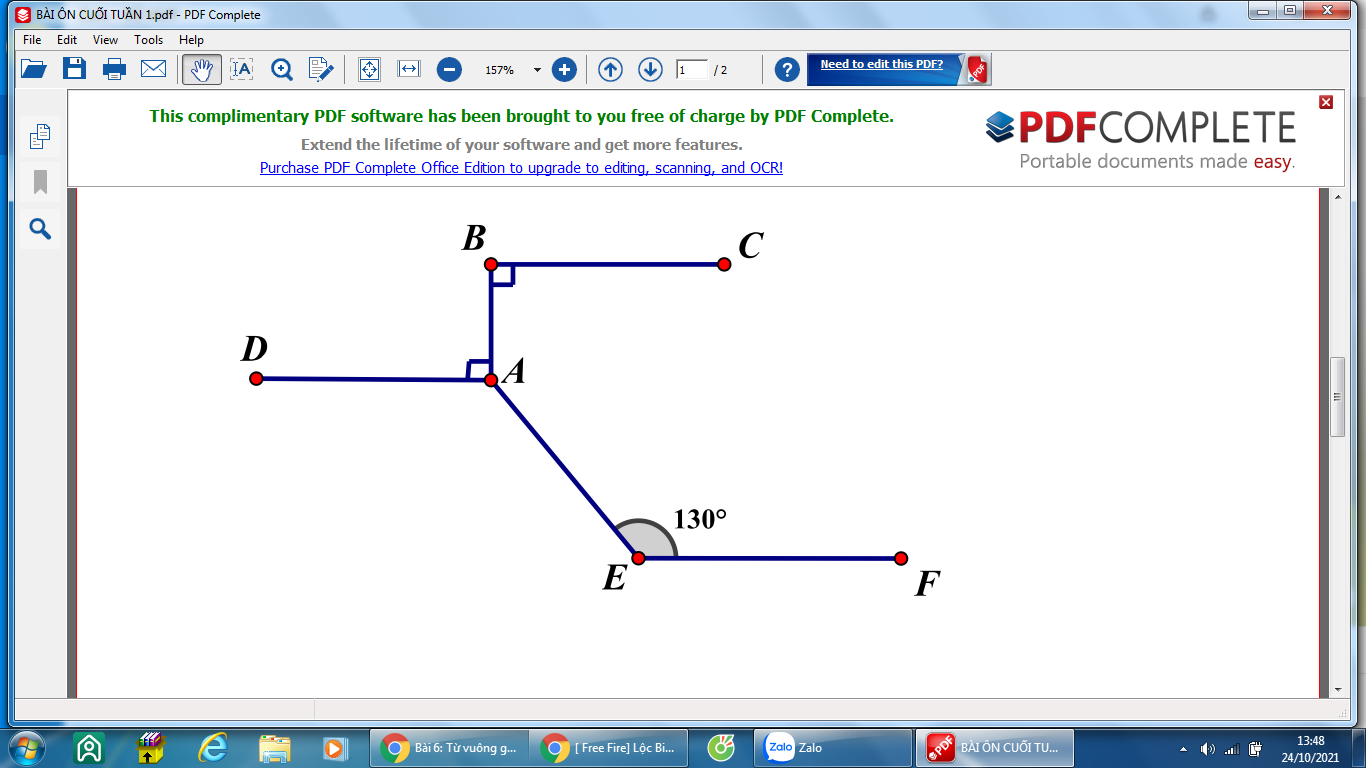
a, Vì BC và AD cùng vuông góc với AB nên BC//AD
Do đó AD//EF
b, \(\widehat{BAE}=360^0-\widehat{BAD}-\widehat{DAE}=360^0-90^0-130^0=140^0\)
21 tháng 3 2021
a, Xét tam giác ABD và tam giác BDC ta có :
^BAD = ^CBD ( gt )
^ABD = ^BDC ( so le trong )
Vậy tam giác ABD ~ tam giác BDC ( g.g )
\(\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}\)( tỉ số đồng dạng ) \(\Rightarrow BD^2=AB.DC=4.9=36\)
\(\Rightarrow BD=\sqrt{36}=6\)cm
b, Gọi giao điểm AC và BD là I
Xét tam giác BIE và tam giác AID có : BE // AD
Theo hệ quả Ta lét ta có : \(\frac{BI}{ID}=\frac{IE}{IA}=\frac{BE}{AD}\)
Xét tam giác AIB và tam giác DIC có AB // CD ( ABCD là hình thang )
\(\frac{AI}{IC}=\frac{IB}{ID}=\frac{AB}{DC}\)
mà \(\frac{BE}{AC}=\frac{AB}{DC}=\frac{IB}{ID}\Rightarrow BE.DC=AB.AC\)
24 tháng 10 2021
b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{EAF}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=EF
T
1 tháng 8 2019
a) Ez bạn tự làm nha, mình làm sơ sơ cũng 3-4 cách rồi.:)
b) Tam giác ABC cân tại A có đường p/g góc A xuất phát từ đỉnh đồng thời là đường trung trực nên \(AD\perp BC\). và BD = CD = BC/2
Xét tam giác ABD vuông tại D (chứng minh trên), theo định lí Pythagoras:
\(AB^2=BD^2+DA^2\Leftrightarrow10^2=\frac{BC^2}{4}+DA^2\)
\(=36+DA^2\Rightarrow AD=8\) (cm) (khúc này có tính nhầm gì thì tự sửa lại nha!)
Theo đề bài ta có AB = AC = 10 < BC = 12
Hay AC < BC. Theo quan hệ giữa góc và cạnh đối diện trong tam giác ABC ta có \(\widehat{ABC}< \widehat{BAC}\) (Cái khúc này không chắc, sai thì thôi)
c) Hướng dẫn:
\(\Delta\)EDB = \(\Delta\)FDC (cạnh huyền - góc nhọn)
Suy ra EB = FC. Từ đó suy ra AE = AF.
Suy ra tam giác AEF cân tại A suy ra \(\widehat{AEF}=\frac{180^o-\widehat{A}}{2}\) (1)
Mặt khác tam giác ABC cân tại A nên \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) suy ra đpcm
a)
Có BC // AD ( cùng vuông góc trên một đường thẳng )
mà BC // EF (giả thuyết)
=>AD // EF ( cùng song song với BC )